Элементарные функции
В таблице 4.2 приведен перечень известных из школьного курса функций и их графиков. Эти функции называются основными элементарными функциями.
Элементарными функциями называются функции, которые можно получить из основных элементарных функций (перечисленных в таблице) с помощью алгебраических операций и композиций функций.
Примеры:
______________________________________________________________________________
1. Функция
у = 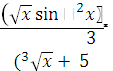 +
+ 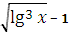
является элементарной, так как она получена с помощью операций сложения, вычитания, умножения, деления и образования сложной функции.
2. Функция у = |x| (рис. 4.4)  является примером неэлементарной функции
является примером неэлементарной функции
у

 y = |x|
y = |x|

х
Рис. 4.4
________________________________________________________________
Таблица 4.2
| Аналитическое задание | Область определения Х | Область значений Y | График |
1. Степенная функция
у = xⁿ ,
n 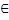 N N
 у = x⁻ⁿ ,
n
у = x⁻ⁿ ,
n 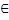 N N
 y =
y = 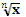 ,
n ,
n 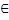 N,
n N,
n 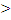 1 1
| (-  , + , +  )
(- )
(-  , 0) , 0) 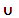 (-
(- 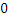 , + , +  )
(- )
(-  , + , +  ),
если n нечетно; ),
если n нечетно;
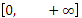 , если n четно , если n четно
| (-  , + , +  ),
Если n нечетно; , если n четно
(- ),
Если n нечетно; , если n четно
(-  , 0) , 0) 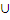 (-
(- 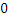 , + , +  ), если n нечетно; ), если n нечетно; 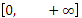 , если n четно
(- , если n четно
(-  , + , +  ),
если n нечетно; ),
если n нечетно;
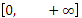 , если n четно , если n четно
|
0 1 х 0 1 х
у =
|
2.Показательная функция
у = 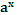 ,
а ,
а 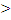 0,
а 0,
а 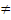 1 1
| (-  , + , +  ) )
| 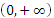
| 
  y
y = y
y = 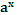 0
0  a a  1
1 a 1
1 a  1 1
 0 1 x 0 1 x
|
| Аналитическое задание | Область определения Х | Область значений Y | График |
3.Логарифмическая функция
y = 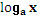 ₁
a ₁
a 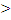 0,
a 0,
a 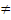 1 1
| ( 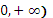
| (-  , + , +  ) )
|
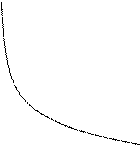  Y Y
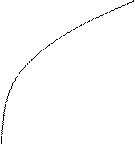 a > 1
y =
a > 1
y = 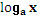
  0 1 x
0 < a < 1
0 1 x
0 < a < 1
|
4.Тригонометрические функции
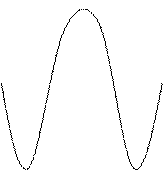
y = sin x
 У = сos x У = сos x
| (-  , + , +  )
(- )
(-  , + , +  ) )
| [-1,1] [-1,1] |  у
у
   
 0 0
 -2П -П П/2 П 2П х
-1 -2П -П П/2 П 2П х
-1
  y y
-п -
|
| y = tg x | (-  + Пn, + Пn,  + Пn),
N + Пn),
N 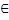 Z Z
| (-  , + , +  ) )
|       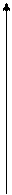 y y
 -п -
-п -  0 0  П x П x
|
Дата добавления: 2015-09-28; просмотров: 537;


 у у
у у
 y =
y = 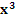
 1
1
 у = х
у = х



 у у
у у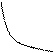

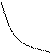 у = 1/x у =1/ х?
у = 1/x у =1/ х?

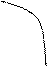
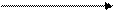
 0 1 x 0 1 x
0 1 x 0 1 x

 у у
у у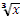 у =
у = 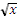



 1 х 0 1 х
1 х 0 1 х
 0
0 

 -1
-1