ЛОГИЧЕСКИЕ ОПЕРАЦИИ

Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.

Логическое отрицание (инверсия) образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно, что …».

Обозначение инверсии: НЕ А; 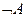; ; 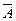NOT A.

Истинность высказывания, имеющего форму 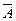(вне зависимости от его содержания), определяется по специальной таблице истинности:

А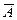

Из таблицы истинности следует, что инверсия высказывания истинна, когда высказывание ложно, и ложна, когда высказывание истинно. Иногда это свойство принимают за определение операции инверсии. В теории множеств логическому отрицанию соответствует операция дополнения к множеству.

Примечания:

1. Логики при образовании инверсии предпочитают иметь дело с оборотом речи «неверно, что», поскольку тем самым подчеркивается отрицание всего высказывания.

2. Дважды или четырежды отрицающееся высказывание имеет то же самое значение истинности, что и исходное высказывание, трижды отрицающееся – что и отрицающееся один раз.

Логическое умножение (конъюнкция) образуется соединением двух высказываний в одно с помощью союза «и».

Обозначение конъюнкции:А И В; 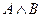; А & B; 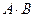; A AND B.

Таблица истинности

А	В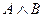

Из таблицы истинности следует, что конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно высказывание ложно. Иногда это свойство принимают за определение конъюнкции. В теории множеств конъюнкции соответствует операция пересечения множеств.

Логическое сложение (дизъюнкция) образуется соединением двух высказываний в одно с помощью союза «или».

Обозначение дизъюнкции: А ИЛИ В; A OR B; А | B; 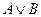; А + В.

Таблица истинности

А	В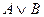

Из таблицы истинности следует, что дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно высказывание истинно. Иногда это свойство принимают за определение операции дизъюнкции. В теории множеств дизъюнкции соответствует операция объединения множеств.

Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если …, то …».

Обозначения импликации: 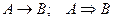. Говорят: если А, то В; А влечет В; В следует из А.

Таблица истинности

А	В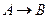

Из таблицы истинности следует, что импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (когда истинная предпосылка ведет к ложному выводу). Иногда это свойство принимают за определение операции импликации. В теории множеств соответствующей операции нет.

Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно при помощи оборота речи «… тогда и только тогда, когда …».

Обозначение эквивалентности: .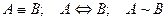

Таблица истинности

Из таблицы истинности следует, что эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба ложны. Иногда это свойство принимается за определение операции эквивалентности. В теории множеств этой операции соответствует операция эквивалентности множеств.

Рассмотренные свойства логических операций можно представить в следующем виде:

Инверсия истинна	Тогда и только тогда, когда	высказывание ложно
Дизъюнкция ложна Конъюнкция истинна	оба высказывания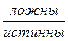
Дизъюнкция истинна Конъюнкция ложна	хотя бы одно высказывание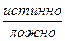
Импликация ложна	из истинного высказывания следует ложное высказывание
Эквивалентность истинна	оба высказывания ложны или оба высказывания истинны