ЛОГИКА КАК НАУКА.
ЛЕКЦИЯ № 4.
ТЕМА: «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ»
ЛОГИКА КАК НАУКА.
Познание истины – одна из важнейших потребностей человека. Каждый человек и человечество в целом стремятся к истине, добру и красоте. Все люди нуждаются в истинном знании, получении новой информации о мире, в котором они живут. Для чего? Для того чтобы жить, что в данном случае означает ориентироваться в быстро меняющейся обстановке, принимать правильные решения и на их основе совершать правильные действия.
Человек с древних времен стремился познать законы правильного мышления, т.е. логические законы. Наука логика помогает познанию этих законов. Законы развития есть у природы, общества, любой сложной системы и, конечно же, у самого мышления. Существуют даже мнение, что всякое движение нашей мысли, постигающей истину, добро и красоту, опирается на логические законы. Мы можем не осознавать их, но вынуждены всегда следовать этим законам, чтобы жить в обществе, общаться с людьми, понимать их и быть понятными.
В Древней Греции, Древней Индии, Древнем Риме законы и формы правильного мышления изучались в рамках ораторского искусства. Применение логических приемов рассуждения позволяло ораторам более убедительно доносить до аудитории их точку зрения, склонять людей на свою сторону. Мыслить логично – значит мыслить точно и последовательно, не допускать противоречий в своих рассуждениях, уметь вскрывать логические ошибки.
Логика – наука о законах и формах рационального мышления, методах формализации содержательных теорий. Мыслить логично – значит мыслить точно и последовательно, не допускать противоречий в своих рассуждениях, уметь вскрывать логические ошибки.
Логика – одна из древнейших наук. Ее основателем считается величайший древнегреческий философ Аристотель, который первым систематизировал формы и правила мышления, обстоятельно исследовал категории «понятие» и «суждение», подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.
Предметом исследования науки логики является человеческое мышление. Мышление всегда осуществляется в каких-то формах. В логике выделяют следующие формы мышления: понятие, суждение, умозаключение. Примеры понятий: 1) апельсин; 2) трапеция; 3) белизна; 4) река Нил; 5) ураганный ветер; 6) студент строительной академии.
Понятие – форма мышления, в которой отражаются отличительные существенные признаки предмета.
Существенными называются такие признаки, каждый из которых, взятый отдельно, необходим, а все вместе достаточны, чтобы с их помощью отличить (выделить) данный предмет (явление) от всех остальных и сделать обобщение, объединение однородные предметы в множество.
Например, признаками понятия апельсин являются: круглый, оранжевый, упругий, сладкий, ароматный. Можно ли по этим признакам отличить апельсин от неапельсина? По ним легко отличить апельсин от яблока, но нельзя отличить апельсин от мандарина: большой мандарин можно спутать с маленьким апельсином. Поэтому для точной идентификации апельсина необходимо вести дополнительные признаки. Понятие имеет две основные логические характеристики: содержание и объем.
Содержание понятие – совокупность существенных признаков, отраженных в этом понятии.
Например, содержанием понятия ромб является совокупность двух существенных признаков: быть параллелограммом и иметь равные стороны.
Объем понятия – множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятия.
Например, объем понятия река – это множество, состоящее из рек, носящих имена Обь, Иртыш, Енисей, Волга, Днепр, Днестр и др. Объем понятия студент включает в себя всех людей, которые когда-либо учились, учатся сейчас или будут учиться когда-нибудь.
Наглядная геометрическая иллюстрация объемов понятий и отношений между ними была предложена математиком, физиком и астрономом Леонардом Эйлером (1707 – 1781) и носит название кругов Эйлера.
Рассмотрим множество студентов некоторой группы (Е). Те студенты, которые занимаются спортом, образуют множество спортсменов (А). Те, кто увлекается литературой, образуют другое множество (В). Те, кто учится на отлично и на каникулах отдыхает в горах, образуют еще одно множество (С). Предположим, что среди студентов, составляющих множество С, нет ни одного, занимающегося спортом, т.е. множества С и А не имеют общих элементов. Множество студентов группы, которые знают пять иностранных языков (D), будет пустым, если таких полиглотов в группе нет. Данную ситуацию графически можно изобразить так:
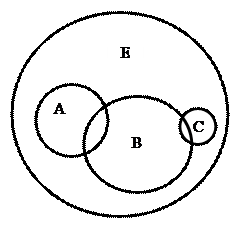
Суждение (высказывание, утверждение) – форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях между ними.
Примеры суждений: 1) Этот апельсин вкусный; 2) Если прошел дождь, то на улице весна; 3) На Луне живут лунатики, а на Марсе – марсиане.
Языковым выражением суждений является повествовательное предложение. Суждения бывают простыми и сложными. Например, Наступила весна – простое суждение, а Наступила весна, и прилетели грачи – сложное, состоящее из двух простых.
Всякое суждение может быть либо истинным, либо ложным по своему содержанию.
Содержание суждения – это то, о чем в нем идет речь, его смысл.
Одно и то же суждение разными людьми может восприниматься как истинное или ложное в зависимости от их взглядов, жизненного опыта, особенностей национальной культуры, воспитания, образования и т.д. Например, для кого-то истинным является, что свободу, безопасность и комфорт дают глубокие знания, а для кого-то – свободу, безопасность и комфорт дают большие деньги.
Для того, чтобы вести рассуждения и оценивать их правильность, необходимо прежде договориться по каждому суждению, будем ли его рассматривать как истинное или ложное в данном конкретном случае. Например, суждение Он – хороший шахматист может быть как истинным, так и ложным, в зависимости от того, кто имеется в виду под местоимением «он». Следует отметить, что «договориться» можно только по отношению к простым суждениям. Значение же истинности сложных суждений вычисляется. При вычислении истинности (ложности) сложного суждения содержание входящих в него простых суждений является незначимым. Интерес представляет то, чем суждения отличаются друг от друга, что характеризует каждое из них и неизменно для каждого из них, а именно их форма.
Логическая форма суждения – это его строение, способ связи его составных частей.
Форма суждения, в отличие от его содержания, объективна, т.е. не зависит от тех или иных взглядов того или иного человека. Следует определить логическую форму следующих суждений: 1) Все лошади едят овес; 2) Все реки впадают в море; 3) Все студенты – отличники; 4) Все книги имеют страницы; 5) Все планеты вращаются вокруг звезд. Во всех этих суждениях говорится о разном (у них различное содержание), но они имеют одинаковую логическую форму: Все S есть P. А суждения Все медузы не имеют головы; Люди не боги имеют другую логическую форму: Все S не есть P.
Умозаключение – форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам вывода получаем суждение-заключение (вывод умозаключения).
В русском языке слово «умозаключение используется в двух значениях: для обозначения процесса рассуждения, размышления, приводящего к некоторому выводу, и для обозначения результата этого процесса. Еще в древности было известно рассуждение, ставшее классическим образцом верного логического умозаключения:
Все люди смертны.
Сократ – человек.
Сократ смертен.
Отметим, что посылками умозаключения по правилам логики могут быть только истинные суждения.
Всякое умозаключение, так же как и суждение, имеет свою форму. Эта форма может быть логически правильной или логически неправильной. Так, в примере с Сократом форма умозаключения логически верная:
Все Sесть P.
Некоторые A есть S.
Некоторые A есть P.
Примеры верных умозаключений:
| УМОЗАКЛЮЧЕНИЕ | ФОРМА УМОЗАКЛЮЧЕНИЯ |
| Четырехугольник (S1), у которого противоположные стороны параллельны (P), есть параллелограмм (S2). Квадрат (S3) – это четырехугольник (S1), у которого противоположные стороны параллельны (P). Квадрат – это параллелограмм. | Если S1 есть P, то S1 есть S2. Все S3 есть S1 и все S3 есть P. Все S3 есть S2. |
| Все граждане Украины имеют право на отдых. Я – гражданин Украины Я имею право на отдых | Все S есть P. A есть S. A есть P. |
| Если цветы поливают, то они не засохнут. Цветы засохли. Цветы не поливали. | Если S есть P1, То S не есть P2. S есть P2. S не есть P1. |
О предметах можно судить верно или неверно, т.е. суждение может быть истинным или ложным. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Примером истинного суждения может служить следующее: «Процессор является устройством обработки информации». Ложным суждение будет в том случае, когда оно не соответствует реальной действительности. Например: «Процессор является устройством печати». Суждение представляет собой относительно законченную мысль, отражающую объекты реального мира с их свойствами и отношениями. В большинстве суждений можно выделить понятие объекта и понятие о свойствах и отношениях этого объекта.
Понятие об объекте называется субъектом и обозначается латинской буквой S, а понятие о свойствах и отношениях объекта называется предикатом и обозначается буквой Р. Оба эти понятия – субъект и предикат называются терминами суждения. Отношения между субъектом и предикатом выражается связками «есть», «не есть», «является», «состоит» и т.д. Именно связка придает суждению его логическую характеристику утверждения или отрицания.
Таким образом, каждое суждение состоит из трех элементов – субъекта, предиката и связки (двух терминов и связки). Состав суждения можно выразить общей формулой «S есть Р» или «S не есть Р». Так, в суждении «Процессор является устройством обработки информации». «Процессор» – субъект, «устройством обработки информации» – предикат, «является» – связка. Суждение выражается в повествовательном предложении. Суждение не может быть выражено повелительным или вопросительным предложением, оценка истинности или ложности которых невозможна.
Правильно ли рассуждает человек, когда говорит:
| УМОЗАКЛЮЧЕНИЕ | ИСТИННОСТЬ СУЖДЕНИЙ | ФОРМА УМОЗАКЛЮЧЕНИЯ |
| Если что-то есть металл, то оно проводит электрический ток. Алюминий проводит ток. Алюминий – металл. | Истина Истина Истина | Если S есть P1, то S есть P2. A есть P2. A есть P1. |
Из истинных посылок получилось истинное заключение. Можно предположить, что, рассуждая по данной форме, получим из истинных посылок истинное заключение во всех случаях. Проверим это:
| УМОЗАКЛЮЧЕНИЕ | ИСТИННОСТЬ СУЖДЕНИЙ | ФОРМА УМОЗАКЛЮЧЕНИЯ |
| Если что-то есть металл, то оно проводит электрический ток. Вода проводит ток. Вода – металл. | Истина Истина Ложь | Если S есть P1, то S есть P2. A есть P2. A есть P1. |
Из истинных посылок получилось ложное заключение. Предположение о том, что, рассуждая по данной форме, всегда из истинных посылок получим истинное заключение, ошибочно. Следовательно, те, кто рассуждает по данной форме, либо ошибаются сами, либо вводят слушателей в заблуждение. Таким образом, услышав какую-нибудь фразу (рассуждение, умозаключение), можно, определив форму этого рассуждения и зная, правильна ли она логически, заранее сказать, будет ли истинным заключение.
Умозаключение – это такая форма мышления, посредством которой из одного или нескольких суждений с необходимостью выводится новое знание о предметах реального мира. Умозаключения бывают дедуктивные, индуктивные и по аналогии.
В дедуктивных умозаключениях рассуждения ведутся от общего к частному. Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» путем умозаключения делается вывод, что «Ртуть электропроводна».
В индуктивных умозаключениях рассуждения ведутся от частного к общему. Например, установив, что отдельные металлы – железо, медь, цинк, алюминий и др. – обладают свойством электропроводности, делается обще заключение, что все металлы электропроводны.
Умозаключение по аналогии переносит знание об одних объектах на другие. Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили, что такой элемент есть и на Земле.
С точки зрения содержания суждений в процессе мышления формируется истинное или ложное отражение мира, а если рассматривать мышлении со стороны формы, то имеет значение только его логическая правильность или неправильность.
Античную логику, основанную Аристотелем, принято называть формальной логикой. Это название происходит от основного принципа логикакак науки, который гласит, что правильность рассуждения (умозаключения) определяется только его логической формой, или структурой, и не зависит от конкретного содержания входящих в него суждений.
Основной принцип формальной логики предполагает, что;
Ø каждое рассуждение, выраженное на некотором языке, имеет содержание и форму;
Ø содержание и форма различаются и могут быть разделены;
Ø содержание не оказывает влияния на правильность рассуждения (поэтому от него можно отвлечься);
Ø для оценки правильности рассуждения существенна лишь его форма;
Ø форму рассуждения необходимо выделить в «чистом» виде и затем на основе только формы решать вопрос о правильности рассуждения.
Постижение науки логики дает возможность узнать законы, правила и приемы мышления, которые помогают анализировать правильность рассуждений, оценивать истинность полученных заключений. Логика изучает формы мышления с точки зрения их структуры, законы и правила получения выводного знания. Логика также изучает приемы, используемые человеком при познании действительности, такие, как абстрагирование, анализ, синтез, обобщение, классификация и др.
По отношению друг к другу понятия делятся на сравнимые и несравнимые.
Дата добавления: 2015-09-11; просмотров: 2177;
