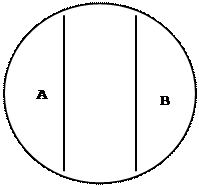
Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (объемы которых не совпадают ни по одному элементу).
Отношение между объемами понятий можно проиллюстрировать с помощью кругов Эйлера. Если имеются два каких-либо понятия X и Y, то объем каждого из этих понятий можно представить в виде круга, а отношение между этими объемами – в виде пары кругов. Выделяют следующие виды отношений между сравнимыми понятиями: равнозначность (тождество), перекрещивание (пересечение), подчинение (субординация), соподчинение, противоположность и противоречие.
Обозначение сравнимых совместимых понятий:
| ТОЖДЕСТВО | ПЕРЕСЕЧЕНИЕ | ПОДЧИНЕНИЕ |

| 
| 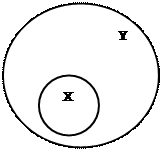 (X подчинен Y)
(X подчинен Y)
|
| X – Ю. Гагарин Y – первый космонавт | X – студент Y - спортсмен | X – лев Y - хищник |
Если два понятия по своим объемам находятся в отношении подчинения, т.е. объем одного понятия входит в объем другого, тогда более широкое по объему понятие называется родовым, а подчиненное видовым.
Так, понятие «компьютер» родовое по отношению к видовому понятию «персональный компьютер», которое, в свою очередь, родовое по отношению к видовому понятию «IBM-совместимый компьютер».
Обозначения сравнимых несовместимых понятий:
| СОПОДЧИНЕНИЕ | ПРОТИВОПОЛОЖНОСТЬ | ПРОТИВОРЕЧИЕ | |||
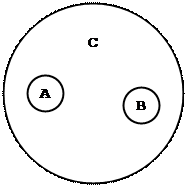 (A и B соподчинены C)
(A и B соподчинены C)
|
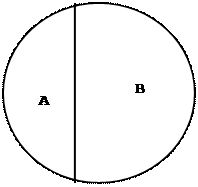
| 
| |||
| A – береза, B – ель, C – дерево. | A – большой дом, B – маленький дом. | A – большой дом, B – небольшой дом. |
Объем понятия – это множество (класс) предметов (элементов множества), каждый из которых характеризуется определенными признаками. Символическая запись 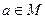 означает: a – элемент множества M. Множество – одно из основных понятий современной математики, используемого почти во всех ее разделах. По словам одного из создателей теории множеств, немецкого математика Георга Кантора, - «Множество есть многое, мыслимое как единое».
означает: a – элемент множества M. Множество – одно из основных понятий современной математики, используемого почти во всех ее разделах. По словам одного из создателей теории множеств, немецкого математика Георга Кантора, - «Множество есть многое, мыслимое как единое».
Дата добавления: 2015-09-11; просмотров: 807;