Основные правила явного определения.

Определения понятий не доказывают и не опровергают. Как оценивают правильность тех или иных определений? Имеются определённые правила и требования, которые необходимо выполнять, формулируя определение данного понятия. Рассмотрим основные из них.

1. Определение должно быть соразмерным. Это означает, что объемы определяемого и определяющего понятий должны совпадать. Если это правило нарушается, в определении возникают логические ошибки: определение оказывается слишком узким (недостаточным) или слишком широким (избыточным). В первом случае определяющее понятие будет меньшим по объёму, чем определяемое понятие, а во втором – большим.

Например, определения «Прямоугольником называется четырехуголь-ник, имеющий прямой угол», «Глаз – это орган зрения человека» - узкое, а определения «Прямоугольником называется четырехугольник, у которого все углы прямые и смежные стороны равны», «Костёр – это источник тепла», «Овощи и фрукты – это источники витаминов» - широкое. Также несоразмерно такое определение квадрата: «Квадратом называется четырехугольник, у которого все стороны равны». Действительно, объём определяемого понятия – множество квадратов, а объём определяющего понятия – множество четырехугольников, все стороны которых равны, а это множество ромбов. Но не всякий ромб есть квадрат, т.е. объёмы определяемого и определяющего понятия не совпадают.

2. Определения не должны содержать «порочного круга». Это означает, что нельзя определять одно понятие через другое, а это другое понятие – через первое.

Например, если определить окружность как границу круга, а круг как часть плоскости, ограниченную окружностью, то мы будем иметь «порочный круг» в определениях данных понятий; если определить перпендикулярные прямые как прямые, которые при пересечении образуют прямые углы, а прямые углы как углы, которые образуются при пересечении перпендикулярных прямых, то мы видим, что одно понятие определяется через другое и наоборот.

3. Определение не должно быть тавтологией, т.е. нельзя понятие определять через само себя, изменяя только (и то зачастую незначительно) словесную форму понятия.

Например, определения: «Перпендикулярные прямые – это прямые, которые перпендикулярны», «Равные треугольники – это треугольники, которые равны», «Касательная к окружности – это прямая, которая касается окружности», «Прямой угол – это угол в 90°», «Сложением называется действие, при котором числа складываются», «Скрипучая дверь – это дверь, которая скрипит», «Холодильник – это место, где всегда холодно» - содержат тавтологию. (Понятие определяется через само себя.)

4. Определение должно содержать указание на ближайшее родовое понятие. Нарушение этого правила приводит к различным ошибкам. Так, учащиеся, формулируя определение, иногда не указывают родовое понятие. Например, определение квадрата: «Это когда все стороны равны». Другой тип ошибок связан с тем, что в определении указывается не ближайшее родовое понятие, а более широкое родовое понятие. Например, определение того же квадрата: «Квадратом называется четырехугольник, у которого все стороны равны».

5. Определение по возможности не должно быть отрицательным. Это означает, что следует избегать таких определений, в которых видовое отличие выступает в качестве отрицательного. Вместе с тем, в математике все же используют такие определения, в частности, если в них указываются свойства, не принадлежащие определяемому понятию. Например, определение «Иррациональное число – число, которое нельзя представить в виде 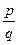, где p и q – целые числа и q≠0».

Последовательность действий, которую мы должны соблюдать, если хотим воспроизвести определение знакомого понятия или построить определение нового: назвать определяемое понятия (термин); указать ближайшее родовое (по отношению к определяемому) понятие; перечислить свойства, выделяющие определяемые объекты из объёма родового, т.е. сформулировать видовое отличие; проверить, выполнены ли правила определения понятия.

Знание вышеперечисленных правил определения понятий даcт возможность учителю более строго относиться к определениям, которые даёт он сам учащимся на уроках, и к определениям, которые дают учащиеся в своих ответах.