Определение понятий. Способы определения понятий

Для распознавания объекта необязательно проверять у него все существенные свойства, достаточно лишь некоторых. Этим пользуются, когда понятию дают определение.

Определить понятие – это значит дать способ, позволяющий отделить объекты, охватываемые данным понятием, от всех других объектов изучения в зависимости от присущих им существенных свойств. Таким образом, определение (лат. «definitio» – «определение») понятий – логическая операция, в процессе которой раскрывается содержание понятия.

Определение понятий – это логическая операция, с помощью которой указываются существенные (отличительные) свойства объекта изучения, достаточные для распознавания этого объекта, т.е. в процессе которой раскрывается содержание понятия либо устанавливается значение термина.

Определение понятия позволяет отличать определяемые объекты от других объектов. Так, например, определение понятия «прямоугольный треугольник» позволяет отличить его от других треугольников.

По способу раскрытия свойств определяемого понятия различают неявные и явные определения. К неявным определениям относятся невербальные определения, к явным - вербальные определения (лат. слово «verbalis» означает «словесный»).

Невербальное определение – это определение значения понятия путём непосредственной демонстрации предметов или указания контекста, в котором применяется то или иное понятие.

Невербальные определения понятий используются в начальном курсе математики, так как младшие школьники обладают преимущественно наглядным мышлением, и именно наглядные представления о математических понятиях играют для них основную роль в обучении математике.

Невербальные определения разделяются на остенсивные (лат. слово «ostendere» – «показывать») и контекстуальные определения.

Остенсивное определение – определение, в котором содержание нового понятия раскрывается путём демонстрации объектов (указания на объекты).

Например.

1. Понятия «треугольник», «круг» «квадрат», «прямоугольник» в дошкольном образовательном учреждении определяются с помощью демонстрации соответствующих моделей фигур.

2. Таким же способом показа можно определить в начальном курсе математики понятия «равенство» и «неравенство».

3 · 5 > 3 · 4 8 · 7 = 56

15 – 4 < 15 5 · 6 = 6 · 5

18+7 >18 17 – 5 = 8 + 4

Это неравенства. Это равенства.

При ознакомлении дошкольников с новыми математическими понятиями в основном используются остенсивные определения.

Однако это не исключает в дальнейшем изучения их свойств, то есть формирования у детей представлений об объёме и содержании понятий, первоначально определенных остенсивно.

Контекстуальное определение – определение, в котором содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл водимого понятия.

Например.

1. Понятия «больше», «меньше», «равно» в начальном курсе математики определяются с помощью указания контекста (больше на 3 – это значит столько же и ещё 3).

2. Примером контекстуального определения может быть определение уравнения и его решения, которые даются во 2 классе. В учебнике математики после записи + 6 = 15 и перечня чисел 0, 5, 9, 10 идет текст: «К какому числу надо прибавить 6, чтобы получилось 15? Обозначим число неизвестное число буквой х (икс): х + 6 = 15 – это уравнение. Решить уравнение – значит найти неизвестное число. В данном уравнении неизвестное число равно 9, т.к. 9+6=15. Объясни, почему числа 0,5 и 10 не подходят».

Из приведенного текста следует, что уравнение – это равенство, в котором есть неизвестное число. Оно может быть обозначено буквой х и это число надо найти. Кроме того, из этого текста следует, что решение уравнения – это число, которое при подстановке вместо х обращает уравнение в верное равенство.

Иногда встречаются определения, сочетающие контекст и показ.

Например.

1. Нарисовав прямые углы, имеющие разное расположение на плоскости, и сделав надпись: «Это – прямые углы», учитель знакомит младших школьников с понятием «прямой угол».

2. Примером такого определения может служить следующее определение прямоугольника. На рисунке дается изображение четырехугольников и приведен текст: «У этих четырехугольников все углы прямые». Под рисунком написано: «Это – прямоугольники».

Таким образом, на начальном этапе обучения учащихся математике чаще всего используются невербальные определения понятий, а именно, остенсивные, контекстуальные и их сочетание.

Необходимо отметить, что невербальные определения понятий характеризуются некоторой незавершенностью. Действительно, определение понятий путем показа или через контекст не всегда указывает на свойства, существенные (отличительные) для данных понятий. Такие определения только связывают новые термины (понятия) с некоторыми объектами или предметами. Поэтому после невербальных определений необходимо дальнейшее уточнение свойств рассмотренных понятий и изучение строгих определений математических понятий.

В средних и старших классах, в связи с развитием языка и накоплением достаточного запаса математических понятий, на смену невербальным определениям приходят вербальные определения понятий. При этом все большую роль начинают играть не наглядные представления о математических понятиях, а их строгие определения. Они основываются на свойствах, которыми обладают определяемые понятия.

Вербальное определение – перечисление существенных (отличительных) свойств данного понятия, сведенных в связное предложение.

В начальном курсе математики изучаемые понятия располагают в таком порядке, чтобы каждое последующее понятие можно было определить, опираясь на ранее изученные их свойства или ранее изученные понятия. Поэтому некоторые математические понятия не определяются (или косвенно определяются через аксиомы). Например, понятия: «множество», «точка», «прямая», «плоскость». Они являются основными, базисными или неопределяемыми понятиями математики. Определение понятий можно рассматривать в виде процесса сведения одного понятия к другому, ранее изученному, и, в конечном счете, к одному из основных понятий.

Например, квадрат есть особый ромб, ромб – особый параллелограмм, параллелограмм – особый четырехугольник, четырехугольник – особый многоугольник, многоугольник – особая геометрическая фигура, геометрическая фигура – точечное множество. Таким образом, мы дошли до основных неопределяемых понятий математики: «точка» и «множество».

В этой последовательности понятий каждое понятие, начиная со второго, является родовым понятием для предыдущего понятия, т.е. объёмы этих понятий находятся между собой в последовательном отношении включения:

Va ÌVв Ì Vc Ì Vd Ì Ve Ì Vf Ì Vq, где а: «квадрат», в: «ромб»,

с: «параллелограмм», d: «четырехугольник», e: «многоугольник»,

f: «геометрическая фигура», q: «точечное множество». Наглядно объемы этих понятий можно изображать и на диаграмме Эйлера-Венна (рис. 7).

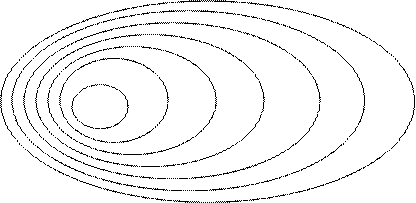V_aV _в V_cV_dV_eV_fV_q

Рис. 7

Рассмотрим основные способы вербальных определений понятий.

I. Определение через род и видовое отличие – самый распространенный вид явных определений.

Например, определение понятия «квадрат».

«Квадратом называется прямоугольник, у которого все стороны равны».

Проанализируем структуру этого определения. Сначала указано определяемое понятие - «квадрат», а затем приведено определяющее понятие, в котором можно выделить две части: 1) понятие «прямоугольник», которое является родовым по отношению к понятию «квадрат»; 2) свойство «иметь все равные стороны», которое позволяет выделить из всевозможных прямоугольников один вид – квадрат, поэтому это свойство называют видовым отличием.

Видовым отличием называются свойства (одно или несколько), которые позволяют выделить определяемое понятие из объема родового понятия.

Следует иметь в виду, что понятия рода и вида относительны. Так, «прямоугольник» – это родовое к понятию «квадрат», но видовое по отношению к понятию «четырехугольник».

Кроме того, для одного понятия может существовать несколько родовых. Например, для квадрата родовыми являются ромб, четырехугольник, многоугольник, геометрическая фигура. В определении через род и видовое отличие для определяемого понятия принято называть ближайшее родовое понятие.

Схематично структуру определений через род и видовое отличие можно представить следующим образом (рис. 8).

Определяемое понятие

Родовое понятие

Видовое отличие

Определяющее понятие

Рис. 8

Очевидно, что определяемое понятие и определяющее понятие должны быть тождественны, т.е. их объёмы должны совпадать.

По данной схеме можно строить определения понятий не только в математике, но и в других науках.

Следующие способы определения понятий являются частными случаями определения через род и видовое отличие.

II. Генетическое или конструктивное определение, т.е. определение, в котором видовое отличие определяемого понятия указывает на его происхождение или способ образования, построения (греч. слово «denesis» – «происхождение», лат. слово «constructio» – «построение»).

Например.

1. Определение понятия «угол».

«Углом называется фигура, образованная двумя углами, исходящими из одной точки». В этом примере понятие «фигура» является родовым, а способ образования этой фигуры – «образована двумя лучами, исходящими из одной точки» - является видовым отличием.

2. Определение понятия «треугольник».

«Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков».

В этом определении указано родовое понятие по отношению к треугольнику – «фигура», а затем видовое отличие, которое раскрывает способ построения фигуры, являющейся треугольником: взять три точки, не лежащие на одной прямой, и соединить каждую их пару отрезком.

III. Индуктивное определение или определение понятия с использованием формулы, позволяющей сформулировать общее отличительное свойство данного понятия (лат. слово «inductio» – «наведение» на рассуждение от частного к общему).

Например, определение понятия «функция прямой пропорциональности».

«Функцией прямой пропорциональности называется функция вида «y=kx, где xÎR, k≠0». В этом примере понятие «функция» - родовое понятие, а формула «y=kx, где xÎR, k≠0» - видовое отличие понятия «функция прямой пропорциональности» от других видов функций.

Рассмотренные способы определения понятий позволяют наглядно изобразить виды определения понятий на следующей схеме (рис. 9).