Отношения между понятиями. Понятия взаимно связаны и взаимно обуславливают друг друга

Понятия взаимно связаны и взаимно обуславливают друг друга. Никакое понятие нельзя усвоить, не осознав его взаимосвязи с другими понятиями. Поэтому важно знать, в каких отношениях могут находиться понятия, и уметь определять эти отношения.

Отношения между понятиями напрямую связаны с отношениями между соответствующими им объёмами.

Условимся обозначать понятия малыми (строчными) буквами латинского алфавита: а, в, с, …, z. Их объёмы будем обозначать соответственно: Va, Vв, Vc, …, Vz.

Пусть заданы понятия а и в, имеющие объёмы Va и Vв. Так как объём понятия – множество, то, устанавливая отношения между объёмами понятий, будем изображать их на диаграммах Эйлера-Венна.

I. Объёмы понятий не пересекаются, т.е. Va ∩ V в = Æ (рис. 3).

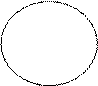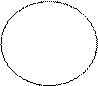V_a Vв

Рис. 3

Если объёмы понятий а и в не пересекаются, т.е. Va ∩ Vв ≠ Æ, то понятия а и в называются несовместимыми или независимыми.

Например, 1) а: «треугольник», в: «отрезок», Va ∩ V в = Æ;

2) а: «дерево», в: «прямая», Va ∩ V в = Æ;

3) а: «существительное», в: «животное», Va ∩ V в = Æ.

II. Объёмы понятий находятся в отношении пересечения, т.е.Va∩Vв ¹Æ (рис. 4).

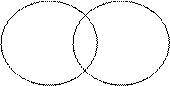
V_a Vв

Рис. 4

Если объёмы понятий а и в находятся в отношении пересечения, т.е. Va ∩ Vв ¹ Æ, то понятия а и в называются совместимыми или зависимыми.

Например, 1) а: «равнобедренный треугольник», в: «прямоугольный

треугольник»; 2) а: «студент», в: «спортсмен»; 3) а: «натуральное число, кратное 3», в: «натуральное число, кратное 4».

III. Объёмы понятий находятся в отношении включения, например, объём понятия в включается в объём понятия а, т.е. Vв Ì Va (иначе, объём понятия в является собственным подмножеством объёма понятия а). Этому случаю соответствует диаграмма, изображенная на рис. 5.

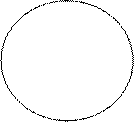V_a

Vв

Рис. 5

Если объём понятия в является собственным подмножеством объёма понятия а, то понятие в называется видовым по отношению к понятию а, а понятие а – родовым по отношению к понятию в.

В этом же случае о понятиях а и в говорят, что: 1) понятие в уже, чем понятие а, а понятие а шире, чем понятие в; 2) понятие в есть частный случай понятия а, а понятие а есть обобщение понятия в.

Например, 1) а: «треугольник», в: «равнобедренный треугольник», Vв ÌVa, следовательно, понятие а является родовым или родом, а понятие в – видовым или видом; 2) а: «многоугольник», в: «треугольник», VвÌVa, а – родовое понятие, в - видовое понятие; 3) а: «часть речи», в: «имя существительное», VaÌVв, а - родовое понятие, в – видовое понятие.

IV. Объёмы понятий находятся в отношении равенства, т.е. Va = Vв

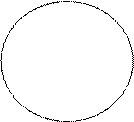(рис. 6).

V_a Vв

Рис. 6

Если объёмы понятий а и в равны, т.е. Va = Vв, то понятия а и в называются тождественными.

Например, 1) а: «квадрат», в: «прямоугольник с равными сторонами»; 2) а: «глаз», в: «око»; 3) а: «окружность», в: «граница круга»; 4) а: «студент», в: «человек, обучающийся в вузе».

Зная, в каких отношениях могут находиться понятия в зависимости от их объёмов, установим, например, отношения между следующими парами понятий а и в, если:

1) а: «прямоугольник», в: «ромб»;

2) а: «многоугольник», в: «четырехугольник»;

3) а: «прямая», в: «треугольник»;

4) а: «параллелограмм с равными сторонами», в: «ромб».

В примере 1 объёмы понятий пересекаются, т.е. Va ∩ Vв ¹ Æ (рис. 4), так как имеют общие элементы: некоторые прямоугольники, а именно, обладающие свойством «имеет все равные стороны», являются ромбами, и некоторые ромбы, а именно обладающие свойством «имеет прямые углы», являются прямоугольниками. Таким образом, понятия «прямоугольник» и «ромб» являются совместимыми или зависимыми.

В примере 2 объёмы данных понятий находятся в отношении включения. Действительно, всякой четырехугольник является многоугольником, но не наоборот, поэтому объём понятия «четырехугольник» является подмножеством объёма понятия «многоугольник», т.е. VвÌVa (рис. 5). Следовательно, понятие «четырехугольник» - видовое по отношению к понятию «многоугольник», а понятие «многоугольник» - родовое по отношению к понятию «четырехугольник».

В примере 3 объёмы понятий не пересекаются, т.е. Va ∩ Vв = Æ (рис. 3), так как ни про одну прямую нельзя сказать, что она является треугольником, и ни один треугольник не может быть назван прямой. Следовательно, понятия «прямая» и «треугольник» являются несовместимыми или независимыми.

В последнем примере объёмы понятий будут равными, т.е. Va= Vв (рис. 6), так как каждый параллелограмм с равными сторонами является ромбом и, наоборот, каждый ромб – это и есть параллелограмм с равными сторонами. Таким образом, понятия «параллелограмм с равными сторонами» и «ромб» являются тождественными.

Замечание.Необходимо отметить, что несовместимые понятия имеют частный случай. Например, если мы установим отношение между понятиями а: «прямая» и в: «отрезок», то их объёмы не пересекаются, т.к. ни одна прямая не может быть названа отрезком, и ни про один отрезок нельзя сказать, что он является прямой. Следовательно, эти понятия являются независимыми или несовместимыми.

В данном случае о понятиях «прямая» говорят, что они находятся в отношении целого и части: отрезок – часть прямой, но не ее вид. Если видовое понятие обладает всеми свойствами родового понятие, то часть не обязательно обладает всеми свойствами целого. Например, отрезок не обладает таким свойством прямой, как ее бесконечность.