ГЛАВА III. ЛОГИКА ПРЕДИКАТОВ

В рамках исчисления высказываний не могут быть обоснованы некоторые виды логических рассуждений. Например:

(*) «Все натуральные числа делятся на 1», «n – натуральное число», «Следовательно, n делится на 1».

Корректность таких умозаключений покоится не только на истинностно-функциональных отношениях между входящими в них предложениями, но и на внутренней структуре самих предложений, а также на понимании таких выражений, как «все», «всякий» и т.д.

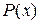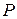Чтобы сделать прозрачной структуру сложных высказываний, удобно ввести специальные обозначения для некоторых часто встречающихся выражений. Если означает, что обладает свойством , то посредством 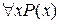будем обозначать утверждение: «Для всякого элемента свойство 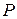выполнено». Запись будет означать высказывание: «Существует элемент , обладающий свойством 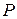». В выражении 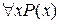часть 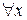называется квантором общности, а часть 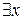в выражении называется квантором существования.

Умозаключение (*) можно теперь записать так:

,

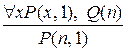где означает, что «натуральное число делится на 1», а означает, что «n – натуральное число».

Основная задача этой главы – научиться представлять в абстрактной форме умозаключения, содержащие кванторы.