Относительная линейная деформация в произвольном направлении
Наметим внутри упругого тела две точки А (х, у, z) и В (х + dx, у + dy, z + dz), находящиеся на расстоянии dr друг от друга (рис. 13). Направляющие косинусы отрезка dr обозначим l, т и п.
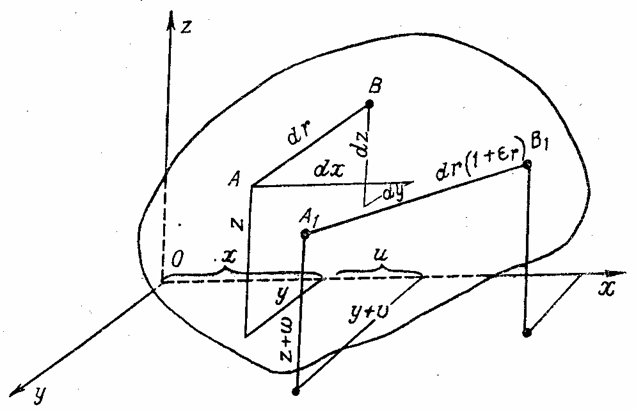
Рис. 13
При деформации тела под влиянием внешней нагрузки, точка А перейдет в положение А1, точка В в положение В1, а отрезок dr получит приращение 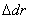 . Новая длина отрезка АВ
. Новая длина отрезка АВ
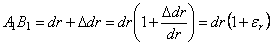 ,
,
где 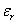 – искомая относительная линейная деформация.
– искомая относительная линейная деформация.
Проекции перемещения АА1 точки А на оси координат обозначаем и, v и w. Тогда проекции перемещения ВВ1 точки В на оси координат и + du, v + dv, w + dw.
С одной стороны
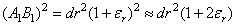 .
.
С другой стороны, квадрат отрезка А1В1 равен сумме квадратов трех его проекций на оси координат:
(А1В1)2 = dx2 + dy2 + dz2 + 2dxdu + 2dydv + 2dzdw.
Тогда получим
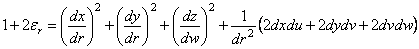 .
.
Подставив выражения для полных дифференциалов перемещений и, v и w, и заметив, что
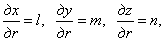
учитывая, что l2 + m2 + п2 = 1, сокращая на 2, и используя зависимости (1.15), получаем
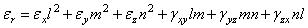 . (1.16)
. (1.16)
Сравнение выражений (1.16) для линейной деформаций 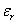 , и (1.6) для нормального напряжения
, и (1.6) для нормального напряжения 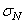 в том же направлении, показывает, что они по структуре одинаковы и выражение (1.16) может быть получено из формулы (1.6) путем замены с сохранением значков
в том же направлении, показывает, что они по структуре одинаковы и выражение (1.16) может быть получено из формулы (1.6) путем замены с сохранением значков 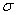 на
на 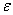 и
и 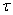 на
на 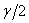 . Пользуясь такой заменой, можно получить все формулы теории деформации из аналогичных формул теории напряжений. В частности, деформированное состояние в точке упругого тела определяется матрицей компонентов тензора деформаций:
. Пользуясь такой заменой, можно получить все формулы теории деформации из аналогичных формул теории напряжений. В частности, деформированное состояние в точке упругого тела определяется матрицей компонентов тензора деформаций:
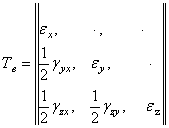 .
.
Дата добавления: 2015-10-26; просмотров: 1310;
