Возможные решения задач теории упругости

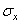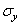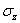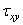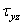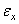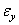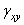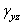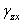В 15 уравнениях (1.2), (1.15), (1.24) являются неизвестными шесть компонентов напряжений ( , , _, , , ), шесть компонентов деформации ( , , _, , , ) и три ком­понента перемещений (и, v, w), т.е. всего 15 неизвестных. Таким образом, с математической точки зрения задача сводится к нахождению 15 функций, удовлетворяющих 15 уравнениям, а также усло­виям на контуре.

При прямом решении задачи, когда в решении участвуют все 15 уравнений, уравнения неразрывности де­формаций, как вытекающие из (1.15) не нужны и могут исполнять роль контрольных уравнений.

Решение указанных трех групп уравнений можно вести разными путями в зависимости от того, что инте­ресует в первую очередь. В связи с этим можно отметить. три направления.

1. Принять за основные неизвестные перемещения точек упругого тела; тогда имеем три неизвестных функции

u = f₁(x,y,z), v = f₂(x,y,z), w =f₃(x,y,z). (1.36)

Для получения решений надлежит в физи­ческие уравнения (1.24) подставить геометрические соотноше­ния (1.15), т. е. выразить напряжения через перемещения, и затем полученные выражения подставить в урав­нения равновесия, в результате чего получим три уравнения

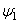(u,v,w)=0, 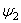(u,v,w)=0, (u,v,w)=0. (1.37)

решение которых приведет к выражениям типа (1.36). Назовем этот метод методом перемещений.

2. Принять за неизвестные напряжения; тогда имеем шесть неизвестных функций

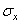= Ф₁(x,y,z), 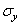= Ф₂(x,y,z), 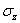= Ф₃(x,y,z),

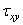= Ф₄(x,y,z), 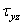= Ф₅(x,y,z), = Ф₆(x,y,z). (1.38)

Так как напряжения из уравнений равновесия непосред­ственно не определяются, надо обратиться к уравнениям деформаций. Используя, например, уравнения неразрывности деформаций (1.17,а) и (1.17,б) с помощью (1.2) и (1.24) можно получить урав­нения в форме:

F₁( 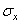,…, 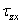) = 0 … F_e( 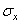,…, 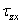) = 0. (1.39)

дальнейшее решение которых приведет к выражениям типа (1.38). Назовем этот метод методом сил.

3. Очевидно, возможен смешанный, метод, когда за ос­новные неизвестные приняты некоторые из перемещений и некоторые из напряжений.

Что касается способов математического решения полу­ченной системы уравнений, то здесь мож­но указать несколько направлений.

а) Точное решение прямой задачи, т. е. непосредствен­ное интегрирование уравнений (1.37) или (1.39).

Основные затруднения при решении прямой задачи теории упругости заключаются обычно в точном удовлетворении ре­шения (1.36) или (1.38) граничным условиям. Эти трудности сни­маются при решении обратной задачи.

б) Решение обратной задачи, является сравнительно простым (так как связано лишь с дифференцированием функций).

Так, например, задаются перемещениями как функциями координат точки (х, у, z) и разыскивают на основании ус­ловий (1.15) деформации, а по ним с помощью (1.24) напряжения; знание последних дает возможность с помощью (1.4) уста­новить поверхностные условия, т. е. внешние нагрузки, которым соответствуют заданные перемещения.

Располагая несколькими решениями обратных задач, каж­дая из которых соответствует своим граничным условиям, можно комбинированием таких решений полу­чить решение и для некоторых прямых задач.

в) Оказался вполне удобным полуобратный способ Сен-Венана, согласно которому задают часть внешних сил и часть перемещений и разыскивают остальные факторы из ус­ловия удовлетворения соответствующих уравнений указанных.выше групп.

Для облегчения решения некоторых уравнений теории упругости оказывается целесообразным способ по­следовательных приближений.

Одной из разновидностей такого способа оказывается использование в некоторых задачах вначале тех решений, которые являются каким-либо элементарным решением, например, найденным в курсе сопротивления ма­териалов. Подстановка этих решений в уравнения теории упругости приводит к некоторым несоответствиям, из анализа которых можно найти путь корректи­ровки предварительного решения, если и не дающий в итоге точного решения задачи, то приводящий к удовлетворитель­ному для практики приближенному решению (более стро­гому, чем исходное элементарное решение).