Закон Гука для изотропного тела
Опытами установлено, что для упругих тел при напряжениях меньше предела упругости компоненты матрицы тензора деформаций Те представляют собой линейные функции составляющих тензора напряжений. Они могут быть в общем случае представлены следующими линейными уравнениями:
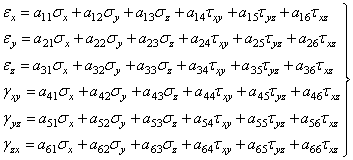 . (1.18)
. (1.18)
Можно доказать, что для системы линейных уравнений (1.18) коэффициенты, расположенные симметрично относительно главной диагонали, должны быть равны: anm = amn. Поэтому в этих уравнениях отпадает (36-6)/2=15 коэффициентов и остается 36 – 15 = 21.
Коэффициенты а11, . . ., а66, число которых 21, зависят от свойств материала и представляют собой упругие постоянные любого анизотропного материала, обладающего различными упругими свойствами в различных направлениях.
Для тела из однородного изотропного упругого материала число произвольных постоянных может быть сокращено. Можно считать, что линейные деформации у этих материалов зависят только от нормальных напряжений, а угловые – только от касательных. Вследствие этого уравнения (1.18) разобьются на две системы из трех уравнений, каждая из которых содержит три неизвестных. Всего останется 18 коэффициентов:
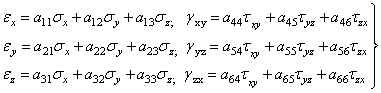 . (1.18,а)
. (1.18,а)
Коэффициенты, расположенные симметрично относительно главных диагоналей, равны друг другу. Поэтому отпадает 2(9-3)/2=6 коэффициентов и остается 18 - 6 = 12.
При заданных напряжениях 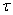 и
и 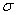 деформации
деформации 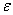 и
и 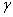 не должны зависеть от выбора осей координат. Это будет соблюдаться, если еще ряд коэффициентов будет равен нулю. Например, при показанном на рис. 15,а направлении касательного напряжения
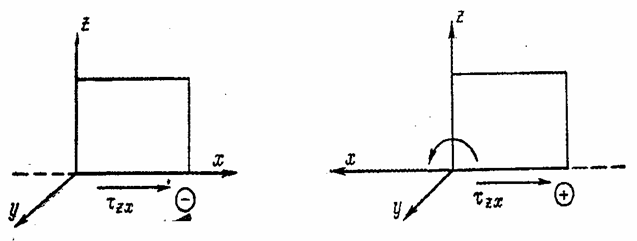
не должны зависеть от выбора осей координат. Это будет соблюдаться, если еще ряд коэффициентов будет равен нулю. Например, при показанном на рис. 15,а направлении касательного напряжения  оно отрицательно. Если же направление оси х изменить на обратное, (рис. 15,б), знак напряжения
оно отрицательно. Если же направление оси х изменить на обратное, (рис. 15,б), знак напряжения  станет положительным и равенство между левой и правой частями четвертого уравнения (1.18а) нарушится.Этого не будет лишь в случае, когда a46 = 0; a64 = 0.
станет положительным и равенство между левой и правой частями четвертого уравнения (1.18а) нарушится.Этого не будет лишь в случае, когда a46 = 0; a64 = 0.
| а | б |
|
Рис. 15
Если повернуть таким же образом ось у, а затем ось z, можно установить, что
a45 = a54 = 0 и а56 = а65 = 0.
Если повернуть одновременно оси х и у по часовой стрелке на 90°, т. е. заменить ось Оу на Ох, а ось Ох на Оу, то в первом уравнении (1.18,а) напряжения 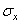 и
и 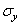 поменяются местами. При этом равенство между левой и правой частями не нарушится лишь при условии а11 = а13. Аналогично во втором и третьем уравнениях (1.18,а) должно быть а21 = а22 и а31 = а32.
поменяются местами. При этом равенство между левой и правой частями не нарушится лишь при условии а11 = а13. Аналогично во втором и третьем уравнениях (1.18,а) должно быть а21 = а22 и а31 = а32.
Если повернуть другие оси, т. е. заменить ось Оу на Оz, затем ось Оz на Ох, можно найти еще равенства
a11 = a22 = a33 и а44 = а55 = а66.
В результате число постоянных для изотропного тела сокращается до трех, известных из курса сопротивления материалов. Из них только две независимы.
Независимыми упругими постоянными могут быть любые две из следующих четырех величин: модуль продольной упругости Е, модуль сдвига G, объемный модуль упругости k и коэффициент поперечной деформации (коэффициент Пуассона) 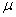 . Они связаны между собой линейной зависимостью
. Они связаны между собой линейной зависимостью
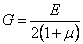 , (1.19)
, (1.19)
а также зависимостью (1.22).
Уравнения, связывающие составляющие тензора деформаций и составляющие тензора напряжений (закон Гука) для однородного изотропного упругого материала, могут быть представлены следующим образом:
1. Известными из курса сопротивления материалов выражениями для составляющих деформаций
 . (1.20)
. (1.20)
2. Выражением, связывающим объемные характеристики. Для этого к первому из уравнений (1.20) прибавим в скобках 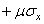 и
и 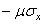 , ко второму
, ко второму 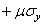 и
и 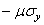 и к третьему
и к третьему 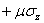 и
и 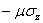 . Сложим все три уравнения и, с учетом формул (1.12) и (1.14), получим
. Сложим все три уравнения и, с учетом формул (1.12) и (1.14), получим
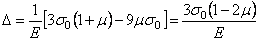
или
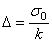 , (1.21)
, (1.21)
где
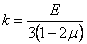 (1.22)
(1.22)
называется объемным модулем упругости.
1. Уравнениями, решенными относительно составляющих напряжений. Для этого первое уравнение (1.20) представим, использовав формулу (1.21), в виде
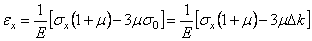 .
.
Решив это уравнение относительно 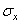 с учетом формулы (1.19), найдем
с учетом формулы (1.19), найдем
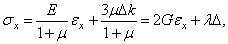
где
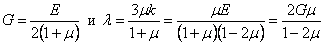 (1.23)
(1.23)
представляют собой величины, зависящие только от упругих постоянных Е и 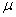 материала, и называются коэффициентами Ламе.
материала, и называются коэффициентами Ламе.
Таким же преобразованием двух следующих уравнений (1.20) получим выражения для 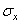 и
и 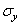 , а решением трех последних уравнений (1.20) - выражения для
, а решением трех последних уравнений (1.20) - выражения для 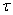 . Итак:
. Итак:
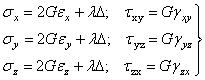 . (1.24)
. (1.24)
Дата добавления: 2015-10-26; просмотров: 2908;
