Уравнения совместности деформаций

Из уравнений (1.15) видно, что если заданы три функции и, v и w, то все шесть составляющих деформаций будут определены однозначно. Но задать эти шесть составляющих произвольно нельзя. Они должны быть связаны дополнительными зависимостями — уравнениями совместности.

Из допущения о сплошности тела следует, что перемещения в его точках должны представлять собой непрерывные и одно­значные функции от координат. Для таких функций величина их производных не зависит от порядка дифференцирования. Поэтому, если дифференцировать по различным переменным ко­ординатам уравнения перемещений, после математи­ческих преобразований можно получить искомые зависимости между составляющими относительных линейных и угловых де­формаций. Так как эти зависимости связаны с условиями сплошности тел, они называются также уравнениями неразрыв­ности.

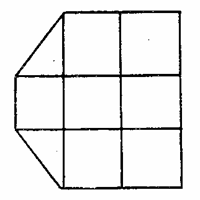
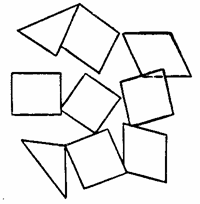
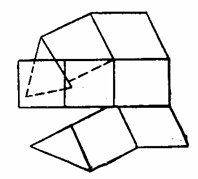
Если эти уравнения не соблюдены, то из малых параллелепи­педов и тетраэдров, на которые можно разделить упругое тело (рис. 14,а), после деформации каждого из них, зависящей от шести составляющих (рис. 14,б), может оказаться невозможным сло­жить непрерывное деформированное тело (рис. 14, в).

а	б	в

Рис. 14

Дифференцируя первые два уравнения (1.15) для линейных деформаций, находим

.

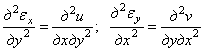Складывая эти выражения и учитывая выражение для угло­вой деформации 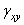, получаем

.

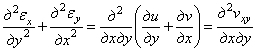Произведя круговую подстановку индексов, можно получить еще два аналогичных уравнения, которые составят первую группу уравнений неразрывности

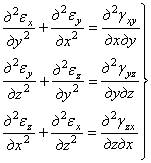. (1.17,а)

Дифференцируем уравнения для угловых деформаций (1.15), складываем первые два уравнения и вычитаем третье:

.

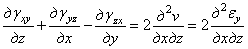Дифференцируем это уравнение по у:

.

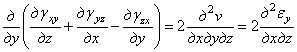После круговой подстановки можно получить еще два анало­гичных уравнения, которые составят вторую группу уравнений неразрывности

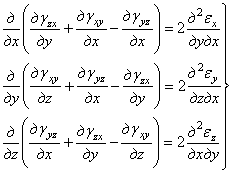. (1.17,б)

Шесть условий (1.17,а) и (1.17,6) будут удовлетво­рены, если при решении задачи теории упругости удастся по заданным нагрузкам, действующим на тело, найти выражения для и, v и w. Если затем вычислить деформации по уравнениям (1.15), то урав­нения совместности, превратятся в тождества, так как они выведены из тех же уравнений (1.15).

Если же при решении задачи по нагрузкам найдем напря­жения, а затем деформации, необходимо проверить, удовлетво­ряют ли найденные деформации уравнениям совместности.

Можно доказать, что уравнения совместности представляют собой необходимые условия для того, чтобы по уравнениям (1.15) можно было найти составляющие перемещения по заданным составляющим деформациям.

Таким образом, зависимости (1.17,а и 17,б) являются необхо­димыми и достаточными условиями интегрируемости формул (1.15), обеспечивающими одновременно однозначность переме­щений. Это справедливо, если тело ограничено односвязной областью, т. е. областью, в пределах которой лю­бая замкнутая кривая может быть непрерывной деформацией стянута в точку без пересечения контура области.