Случай температурного поля
Если элементарный параллелепипед, предположить подверженным только тепловому воздействию, то его деформация характеризовалась бы следующими компонентами:
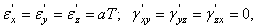
где а – коэффициент линейного теплового расширения и Т — температура. Будем полагать, что рассматриваемое температурное поле не слишком высокое, чтобы могли измениться упругие характеристики материала (в частности - модуль упругости).
При одновременном наличии компонентов напряжений и теплового эффекта, компоненты деформации, используя (1.20), запишем так:
 . (1.45)
. (1.45)
Если в первых трех выражениях аТ перевести в левую часть равенств и обозначить
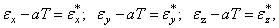
то уравнения (1.45) примут вид, сходный с (1.20) с заменой 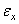 на
на 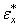 ,
, 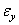 на
на 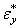 и
и  на
на 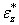 .
.
В таком случае можно использовать вариант обобщенного закона Гука. Тогда получим:
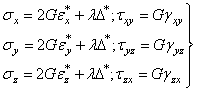 . (1.46)
. (1.46)
где 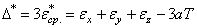 .
.
Компоненты уравнений теории упругости для решения такой задачи будут складываться из прежних дифференциальных уравнений равновесия (1.2), прежних геометрических уравнений (1.15), прежних условий на границе (1.4) и новых физических уравнений (1.45) или (1.46), составленных для случая теплового эффекта.
Эти уравнения можно переписать в виде:
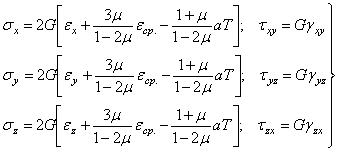 . (1.47)
. (1.47)
Если теперь проделать выкладки, как в разделе 1.13, то взамен (1.42) придем к уравнениям
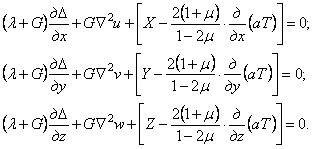 (1.48)
(1.48)
Сравнивая (1.48) с (1.47), можно заключить, что при вычислении перемещений неравномерность нагрева тела как бы равносильна добавлению к реальным объемным силам (X, Y, Z) некоторых фиктивных объемных сил, пропорциональных градиентам температур, т. е. пропорциональных 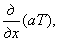
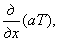
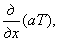 а при вычислении напряжений (1.47) появлению дополнительных членов, пропорциональных температуре.
а при вычислении напряжений (1.47) появлению дополнительных членов, пропорциональных температуре.
Краткие выводы
1. Цель математической теории упругости – определить напряжения и деформации при любых нагрузках на границе и внутри упругого тела любой форы.
В отличие от сопротивления материалов, базирующегося на гипотезе плоских сечений и других упрощенных предположениях, теория упругости ставит целью относительно строгое решение задачи при минимальном количестве исходных гипотез.
Задачей точного решения в теории упругости является получение такой системы функций напряжений, смещений и деформаций, чтобы в каждой точке внутри тела были обеспечены условия равновесия и условия непрерывности (сплошности) тела, а у границы тела внутренние силы находились бы в равновесии с внешними силами, действующими на поверхностях (на границе) тела.
2. Для этой цели теория упругости располагает следующими группами уравнений:
а) тремя статическими, уравнениями, справедливыми для каждой точки внутри тела, из которых следует, что интенсивности изменения (градиенты) нормальных и касательных напряжений вдоль координатных осей и сами напряжения между собой не являются независимыми и подчинены определенным дифференциальным соотношениям (1.2).
б) шестью геометрическими уравнениями (1.15), справедливыми для каждой точки внутри тела, из которых, с одной стороны, следует, что компоненты деформации (удлинения и сдвиги) связаны дифференциальными соотношениями с функциями смещений, а с другой стороны (как следствие), интенсивности изменения деформаций вдоль координатных осей и сами деформации между собой не являются независимыми и подчинены определенным дифференциальным соотношениям, именуемым уравнениями неразрывности деформации (1.17,а) и (1.17,б).
в) шестью физическими уравнениями (1.24), справедливыми для каждой точки внутри тела и связывающими компоненты напряжений в каждой точке с компонентами деформации для той же точки.
Иначе говоря, в каждом конкретном теле (со своими упругими характеристиками) указанные непрерывные функции для компонентов напряжений, деформаций и смещений оказываются взаимосвязанными, т. е. существует связь не только между функциями, входящими в каждую отдельную группу, но одной группы уравнений с уравнениями другой группы. Эта взаимосвязь предопределяется физической природой исследуемого тела.
3. В указанные три группы уравнений, составляющие в итоге пятнадцать уравнений, входят пятнадцать неизвестных функций. Принципиально может быть найдено бесчисленное множество решений, каждое из которых обратило бы в тождество все перечисленные уравнения, т. е. обеспечило бы равновесие и непрерывность тела в окрестности любой точки внутри тела. Однако каждое из таких решений соответствовало бы своим особым статическим условиям (внешним нагрузкам) и кинематическим условиям на поверхности тела (наличие или отсутствие тех или иных связей). Поэтому истинным решением задачи будет то, которое увязано с конкретными, заданными граничными условиями и потому конкретное решение должно удовлетворять действительным граничным условиям. Часто эти условия задаются в статическом плане и для каждой точки на границе тела представляются тремя граничными условиями (1.4).
Задача №1
На гранях параллелепипеда замерены напряжения (см. таблицу). Аналитически и графически определить главные напряжения и главные площадки, вычислите 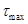 и главные деформации.
и главные деформации.
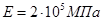 ,
, 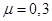 .
.
| 1я цифра шифра | 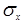
| 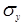
| 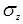
| 2я цифра шифра | 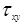
| 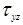
| 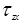
|
| -10 | |||||||
| -20 | -35 | ||||||
| -15 | -20 | ||||||
| -25 | |||||||
| -15 | -45 | ||||||
| -25 | |||||||
| -45 | |||||||
| -40 | -25 | ||||||
| -25 | |||||||
| -35 | -25 |
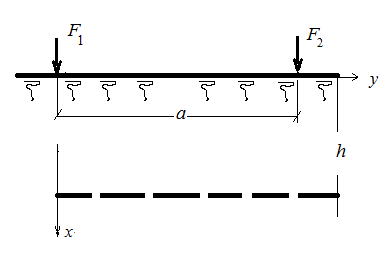
Задача №2
Полуплоскость загружена силами 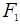 и
и 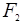 . В уровне «h» на отрезке «а» постройте эпюры напряжений
. В уровне «h» на отрезке «а» постройте эпюры напряжений 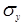 и
и 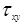 , в точке
, в точке 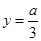 вычислите горизонтальное нормальное напряжение и исследуйте напряженное состояние.
вычислите горизонтальное нормальное напряжение и исследуйте напряженное состояние.
| 1я цифра шифра | 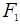
| 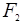
| 2я цифра шифра | а | h |
Дата добавления: 2015-10-26; просмотров: 938;
