Плоская задача в полярных координатах
Если тело имеет форму кругового цилиндра или ограничено радиальными и круговыми сечениями цилиндра, плоскую задачу проще решать не в прямоугольных, а в полярных координатах.
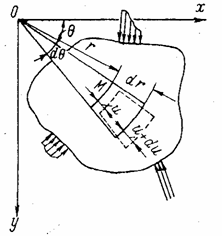
Выделим у точки М тела произвольной формы, имеющего постоянную толщину в направлении оси z, равную единице, и находящегося под действием взаимно уравновешивающихся нагрузок (рис. 17,а), элемент двумя радиальными и двумя окружными сечениями и составим условия его равновесия. На элемент действуют радиальные и окружные нормальные напряжения 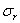 и
и 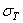 касательные напряжения
касательные напряжения 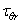 и
и 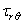 . Действующие по граням выделенного элемента напряжения, с учетом их приращения вследствие изменения переменных
. Действующие по граням выделенного элемента напряжения, с учетом их приращения вследствие изменения переменных 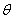 и r, показаны на рис. 17,б.
и r, показаны на рис. 17,б.
| а | б | |
| 
| |
| в | г | |
| 
| |
Рис. 17
Составим уравнения равновесия, приравняв нулю суммы проекций всех сил, действующих на элемент, на биссектрису R угла 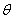 и на касательную Т к окружности радиусом
и на касательную Т к окружности радиусом 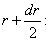

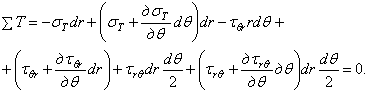
Выполняя перемножение, откидывая величины высшего порядка малости, сокращая подобные члены и деля на 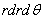 , получаем по этим формулам дифференциальные уравнения равновесия в полярных координатах
, получаем по этим формулам дифференциальные уравнения равновесия в полярных координатах
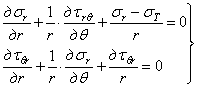 . (1.32,а)
. (1.32,а)
Учитывая, что 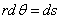 находим, что первые два члена в уравнениях (1.32,а) и (1.29) соответствуют друг другу. Последние члены в каждом из уравнений (1.32,а) выражают особенности полярных координат по сравнению с прямоугольными. Чем ближе элемент к началу координат, тем они больше. Для точки в начале координат при r = 0 уравнения (1.32,а) неприменимы.
находим, что первые два члена в уравнениях (1.32,а) и (1.29) соответствуют друг другу. Последние члены в каждом из уравнений (1.32,а) выражают особенности полярных координат по сравнению с прямоугольными. Чем ближе элемент к началу координат, тем они больше. Для точки в начале координат при r = 0 уравнения (1.32,а) неприменимы.
Закон Гука для плоского напряженного состояния
 . (1.33)
. (1.33)
Для плоского деформированного состояния модуль упругости Е, модуль сдвига G и коэффициент Пуассона 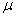 в формулах (1.33) заменяются приведенными величинами Е', G' и
в формулах (1.33) заменяются приведенными величинами Е', G' и 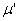 .
.
Уравнение совместности в полярных координатах при постоянных объемных силах получается из уравнения (1.31,а) путем перехода от декартовых координат к полярным. Координаты r и 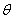 можно представить в виде функций координат х иу:
можно представить в виде функций координат х иу:
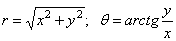 .
.
Поэтому первые частные производные какой-либо функции r и 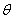 по х и у
по х и у
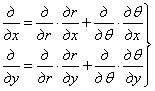 .
.
Пользуясь выражениями для r и 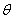 , вычисляем входящие в последние формулы производные и после подстановки этих производных, получаем
, вычисляем входящие в последние формулы производные и после подстановки этих производных, получаем
 .
.
Дифференцируя эти выражения, находим вторые производные. Складывая эти производные, получаем для первой скобки уравнения (1.31,а)
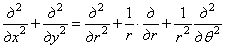 .
.
Для того, чтобы выразить вторую скобку уравнения (1.31,б) в напряжениях 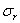 и
и 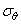 , соответствующих полярным координатам, воспользуемся формулой (1.6). Площадки, по которым действуют нормальные напряжения
, соответствующих полярным координатам, воспользуемся формулой (1.6). Площадки, по которым действуют нормальные напряжения 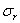 и
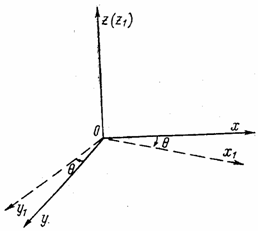
и 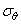 , находим, поворачивая оси координат х и у на угол
, находим, поворачивая оси координат х и у на угол 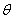 вокруг оси z, как показано на рис. 17,в. Направляющие косинусы для повернутых осей даны в табл. 2.
вокруг оси z, как показано на рис. 17,в. Направляющие косинусы для повернутых осей даны в табл. 2.
Таблица 2
| Оси | x | y | z |
| х1 | l1 = cos 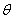
| m1 = sin 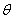
| n1 = 0 |
| у1 | l2 = - sin 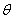
| m2 = cos 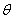
| n2 = 0 |
| z1 | l3 = 0 | m3 =0 | n3 = 1 |
Подставляя в формулу (1.6) соответствующие значения косинусов, получаем для напряжений в полярных координатах (рис. 17,г)
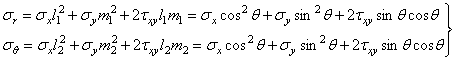 .
.
Сложение этих формул показывает, что 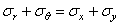 . Тогда уравнение совместности (1.31,б) в полярных координатах принимает вид
. Тогда уравнение совместности (1.31,б) в полярных координатах принимает вид
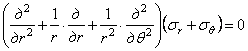 . (1.34,а)
. (1.34,а)
Если объемные силы имеют потенциал, все три составляющих напряжения 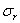 ,
, 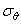 и
и 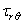 в полярных координатах могут быть выражены через одну функцию
в полярных координатах могут быть выражены через одну функцию 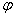 (r,
(r, 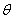 ) напряжений. При отсутствии объемных сил, напряжения выражаются через функцию j следующим образом:
) напряжений. При отсутствии объемных сил, напряжения выражаются через функцию j следующим образом:
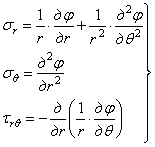 .
.
При подстановке этих выражений в дифференциальные уравнения (1.32,а) последние превращаются в тождества.
Уравнение совместности (1.34,а), выраженное через функцию напряжений, примет вид
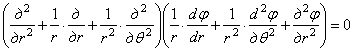 . (1.34,б)
. (1.34,б)
В случае осесимметричной плоской задачи при нагрузке, симметричной относительно оси z, касательные напряжения по граням элемента отсутствуют и дифференциальные уравнения равновесия (1.32,а) имеют вид
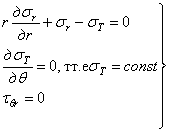 . (1.32,б)
. (1.32,б)
Перемещение в случае осесимметричной плоской задачи происходит только в радиальном направлении (и на рис. 17, а) и не зависит от 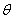 . В окружном направлении в этом случае перемещение отсутствует.
. В окружном направлении в этом случае перемещение отсутствует.
Относительная линейная деформация в радиальном направлении
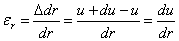 . (1.35,а)
. (1.35,а)
Относительная линейная деформация в окружном направлении
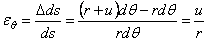 . (1.35,б)
. (1.35,б)
Относительный сдвиг 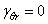 .
.
Дата добавления: 2015-10-26; просмотров: 2024;
