Плоская задача в прямоугольных координатах

Большая категория задач теории упругости допускает значительное упрощение математического реше­ния. Это задачи, в которых можно считать, что внешние воздей­ствия лежат в плоскостях, параллельных какой-либо плоскости хОу, и что вызываемые ими напряжения и перемещения одинаковы для всех точек любой оси z, перпендикулярной этой плоскости. Напряжения по площадкам хОу и перемещения по направлению оси z или отсутствуют, или представляют собой функции напря­жений и перемещений, возникающих в плоскости хОу. Такие за­дачи объединяются общим названием — плоские задачи. Разли­чают две разновидности плоской задачи: плоское деформированное и плоское напряженное состояния.

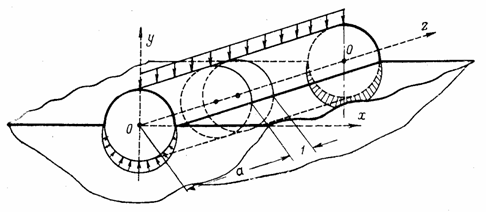
При плоском деформированном состоянии точки тела не могут перемещаться вдоль оси z (рис.16,а) из-за препятствия со сто­роны соседних элементов (вдали от торцов при большой длине тела). Нагрузка, действующая на тело, постоянна вдоль оси z, но может меняться в плоскости хОу при условии, что она в этой плоскости уравновешена. В таком случае любой элемент толщи­ной, равной единице, вырезанный двумя параллельными сече­ниями, перпендикулярными оси z, на известном расстоянии z = а от торцов (рис. 16,б) находится в одинаковых условиях с сосед­ними и испытывает плоское деформированное состояние. Пере­мещения w вдоль оси z отсутствуют (w = 0), а два других (и и v) не зависят от координаты z.

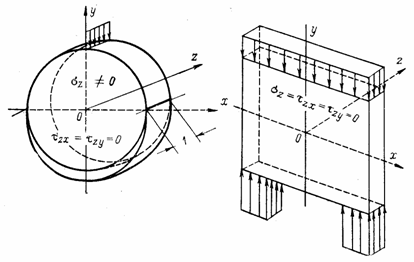
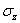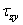При плоском напряженном состоянии размеры тела вдоль оси z малы (рис. в), а боковые плоскости хОу свободны от нагрузки, т.е. напряжения , и этим плоскостям равны нулю. Ввиду малой толщины можно предположить, что и внутри тела, по плоскостям, параллельным хОу, напряжения пренебрежимо малы, а напряжения 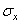, 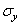и 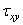не зависят от координаты z. Перемещения 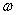вдоль оси z происходят, но они представляют собой функцию напряжени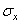й и .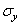

Основные уравнения теории упругости, применительно к указанным разновидностям плоской задачи упростятся следующим образом:

1. Плоское деформированное состояние.

Перемещения и = f₁(x, y), v = f₂(x, y) и w = 0.

Деформации из уравнений Коши (1.15)

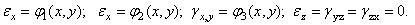
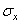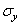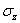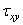Напряжение , , и не равны нулю; .

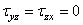Перейдем к уравнениям закона Гука. По третьей формуле (1.20)

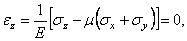
откуда

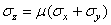, (1.25)

т.е. напряжение .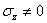

Подставив в формулу (1.20) выражение (1.25), получим

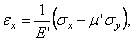
где приведенный модуль упругости

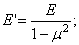
приведенный коэффициент Пуассона

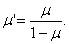
а
б	в

Рис. 16

Аналогично можно преобразовать вторую формулу (1.20).

Приведенный модуль сдвига

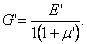(1.26)

Таким образом,

(1.27)

2. Плоское напряженное состояние.

Перемещения u =f₁(x,y); v = f₂(x,y) и w = f₃(x,y).

Деформации 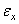= 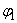(x, y); 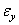= 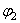(x, y); = 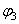(x, y);

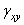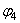= (x, y); .

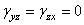Напряжения 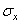, 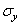и 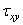не равны нулю; .

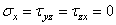Уравнения закона Гука

(1.28)

3. Уравнения, одинаковые для плоского деформированного и напряженного состояний.

Из трех уравнений равновесия (1.2) ввиду того, что все напряжения не зависят от z, a 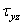и равны нулю, остается два:

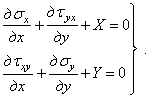(1.29)

Условия на поверхности (1.4) примут вид

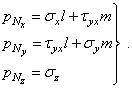(1.30)

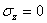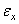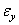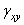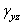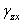Для плоского напряженного состояния p_Nz = 0, так как . Из шести уравнений совместности (1.16) вследствие того, что , и не зависят от z, равно нулю или тоже не зависит от z, а и равны нулю, останется одно

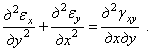(1.31,а)

Если в уравнении (1.31,а) заменить деформации напряжениями, пользуясь формулами (1.28), и получившуюся в правой части уравнения удвоенную производную 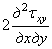заменить выраже­нием

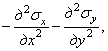
полученным из уравнений (1.29) при условии отсутствия объемных сил, то уравнение совместности деформации может быть представлено в напряжениях

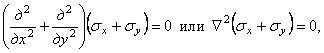(1.31,б)

где 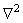– оператор Лапласа.

Путем совместного решения уравнений (1.29) и (1.31,б) могут быть найдены напряжения в случае плоской задачи. Так как в эти уравнения не входят упругие постоянные, можно заключить, что напряженное состояние не зависит от материала.

В случае, если объемные силы имеют потенциал, три состав­ляющих напряжения 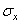, 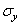и 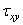могут быть выражены через одну функцию, называемую функцией напряжений. Если объемная сила имеет только одну проекцию 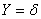(например, собственный вес), то три составляющих напряжения выражаются через функ­цию напряжений следующим образом:

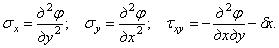
Можно убедиться, что эти выражения удовлетворяют уравнениям равновесия (1.29). Подставив в уравнение (1.31,б), получим бигармоническое уравнение плоской задачи

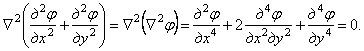
Решение плоской задачи сводится к подысканию функции 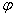, удовлетворяющей этому уравнению и условиям на поверхности.