Нормальное падение плоской электромагнитной волны на диэлектрическое полупространство
Предположим, что полупространство 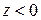 декартовой системы координат (область 1) представляет собой вакуум:
декартовой системы координат (область 1) представляет собой вакуум: 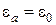 ,
, 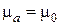 ,
, 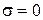 , а полупространство
, а полупространство 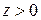 (область 2) представляет собой произвольный диэлектрик с параметрами
(область 2) представляет собой произвольный диэлектрик с параметрами 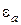 ,
, 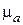 ,
, 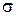 (рисунок 62).
(рисунок 62).
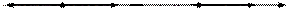
Рисунок 62 − Падение плоской волны на диэлектрическое полупространство
Пусть в области 1 по направлению положительной оси 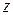 распространяется плоская электромагнитная волна, которую будем называть падающей. Для падающей волны заданы векторы
распространяется плоская электромагнитная волна, которую будем называть падающей. Для падающей волны заданы векторы 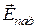 и
и 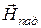 , ориентированные так, как это показано на рисунке. Комплексные амплитуды векторов записываются следующим образом:
, ориентированные так, как это показано на рисунке. Комплексные амплитуды векторов записываются следующим образом:
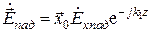 ,
,
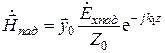 ,
,
где 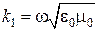 − постоянная распространения плоских волн в вакууме,
− постоянная распространения плоских волн в вакууме, 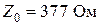 − волновое (характеристическое) сопротивление вакуума.
− волновое (характеристическое) сопротивление вакуума.
Естественно предположить, что в данной системе помимо падающей существуют еще две волны: отраженная
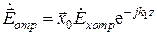 ,
,
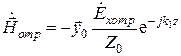 ,
,
где знак вектора магнитного поля обусловлен тем, что вектор Пойнтинга отраженной волны 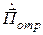 направлен в сторону отрицательной оси
направлен в сторону отрицательной оси 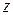 .
.
Вторая волна − прошедшая (преломленная), характеризуемая векторами
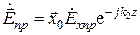 ,
,
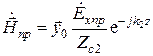 .
.
Здесь 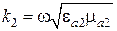 ,
, 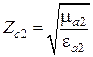 − соответственно постоянная распространения и характеристическое сопротивление среды 2.
− соответственно постоянная распространения и характеристическое сопротивление среды 2.
При записи выражений для прошедшей волны предполагается, что, с одной стороны, область 2 не ограничена по оси 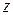 , а с другой, что есть хотя бы сколь угодно малое, но конечное затухание электромагнитных волн при распространении в данной среде. Данные предположения обеспечивают отсутствие отраженных волн в области 2, идущих по направлению отрицательной оси
, а с другой, что есть хотя бы сколь угодно малое, но конечное затухание электромагнитных волн при распространении в данной среде. Данные предположения обеспечивают отсутствие отраженных волн в области 2, идущих по направлению отрицательной оси 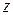 .
.
Необходимо найти соотношения между амплитудами векторов электромагнитного поля падающей, отраженной и прошедшей волн. Для этого следует учесть, что на границе раздела, т.е. в плоскости 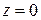 должны выполняться граничные условия непрерывности тангенциальных составляющих суммарных векторов электрического и магнитного полей:
должны выполняться граничные условия непрерывности тангенциальных составляющих суммарных векторов электрического и магнитного полей:
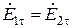 ,
, 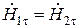 , при
, при 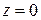 .
.
На основании выражений для падающей, отраженной и преломленной волн граничное условие запишется в виде:
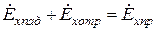 ,
,
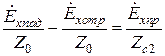 .
.
Введем коэффициент отражения по электрическому полю 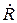 и коэффициент прохождения по электрическому полю
и коэффициент прохождения по электрическому полю 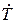 согласно соотношениям:
согласно соотношениям:
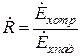 ,
, 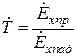 .
.
Разделив левые и правые части равенств на амплитуду электрического поля падающей волны 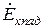 , получим систему двух линейных алгебраических уравнений относительно
, получим систему двух линейных алгебраических уравнений относительно 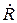 и
и 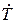 :
:
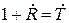 ,
, 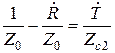 ,
,
откуда
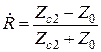 ,
, 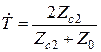 .
.
Таким образом, коэффициенты отражения и преломления для диэлектрического полупространства полностью определяются характеристическими сопротивлениями граничащих сред. Весьма интересно отметить, что формулы этого же вида встречаются в курсе теории цепей при рассмотрении отражения от стыка двух линий с распределенными постоянными, обладающих волновыми сопротивлениями 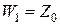 и
и 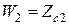 .
.
Дата добавления: 2015-10-19; просмотров: 1849;
