Волны типа Е в круглом волноводе

Задача о распространении по круглому металлическому волноводу колебаний электрического типа, характеризующихся условиями 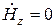, , 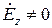сводится к решению уравнения Гельмгольца

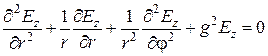
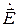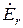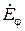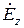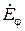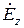при граничных условиях, обеспечивающих обращение в нуль тангенциальных составляющих электрического вектора на стенках волновода. Очевидно, что из трех возможных составляющих поля , а именно: , , касательными к стенкам волновода могут быть только составляющие и . Поэтому необходимо потребовать

,

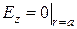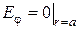
Из формул перехода от продольных составляющих к поперечным непосредственно следует, что два последних условия не являются независимыми. Так, составляющая 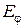. пропорциональная частной производной 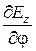, обратится в нуль при постоянстве 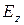на контуре волновода. Поэтому физичски достаточно, чтобы на металлических стенках волновода выполнялось граничное условие 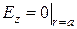. Вместе с уравнением Гельмгольца оно образует однородную краевую задау Дирихле.

Будем решать эту задачу методом разделения переменных. Положим, что

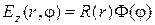
где 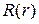, 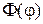− неизвестные функции только от 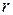и 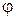соответственно, подлежащие определению.

Подставляя последнее выражение в уравнение Гельмгольца, будем иметь

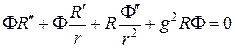
Преобразуем это уравнение таким образом, чтобы в левой части располагались функции только от 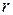, а в правой—только от 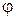. Для этого левую и правую части следует разделить на произведение :

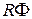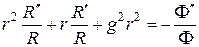
Для того чтобы это уравнение выполнялось тождественно при любых 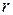и 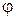, необходимо выполнение равенства

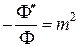
Решением этого уравнения служат равенства

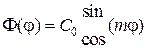
а также их любая линейная комбинация при произвольном коэффициенте 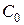. Выбор той или иной из этих функций безразличен в силу симметрии волновода по угловой координате 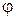. Однако для того чтобы выполнялось физически очевидное требование периодичности решения по углу 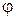с периодом не более 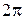, 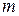должно быть целым числом или нулем (в последнем случае приемлемо только косинусоидальное решение).

Число 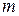служит одним из индексов типа волны

Рассмотрим теперь левую часть волнового уравнения с целью получить новое уравнение, описывающее радиальное распределение поля. Из последних выкладок имеем

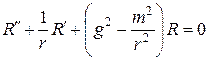
Целесообразно преобразовать это уравнение к несколько другому виду, введя безразмерную независимую переменную

,

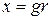откуда получим

.

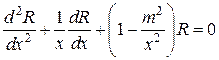Данное уравнение хорошо изучено в математической физике и носит название уравнения Бесселя. С математической точки зрения уравнение Бесселя является линейным дифференциальным уравнением второго порядка с переменными коэффициентами.

Цилиндрические функции. Так называют частные решения уравнения Бесселя. К ним относятся:

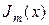— функция Бесселя или цилиндрическая функция первого рода индекса ;

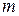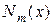— функция Неймана или цилиндрическая функция второго рода индекса .

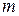Обе цилиидрические функции являются линейно независимыми, поэтому общее решение уравнения Бесселя записывается в виде

,

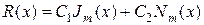где 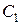и 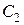— некоторые произвольные постоянные.

Цилиндрические функции первого и второго рода в цилиндрической системе координат играют ту же роль, что синусоидальная и косинусоидальная функции в декартовой прямоугольной системе. Из примерного вида графиков этих функций, представленного на рисунке 30, видно, что они имеют много общего с гармоническими функциями. Однако имеются и существенные различия:

1) цилиндрические функции в отличие от синусоидальной и косинусоидальной не являются периодическими;

2) амплитуда этих функций также не постоянна, а уменьшается с ростом независимой переменной ;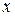

3) чем больше индекс 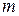, тем сильнее смещены цилиндрические функции по оси 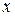; на рисунке это показано применительно к функциям 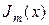и ;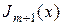

4) вблизи начала координат функция 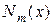неограниченно велика:

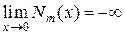
Поэтому при решений задач в круглых волноводах необходимо полагать 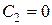, ибо присутствие на оси волновода при 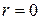бесконечно высоких напряженностей полей физически нереально.

Для решения большинства практических задач наибольший интерес представляют простейшие цилиндрические функци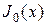и и 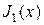. В теории цилиндрических функций показано, что между ними существует следующее соотношение:

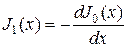
На рисунке 30 представлены графики этих функций. Для дальнейшего наибольший интерес представляют те значения аргумента, при которых обращаются в нуль сами функции Бесселя, либо первые производные. Введем следующие обозначения:

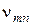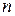— -й корень уравнения ,

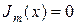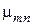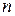— -й корень уравнения .

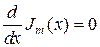Анализируя представленные графики, легко видеть, что функция 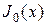первый раз пересекает ось абсцисс в точке, приблизительно равной 2,405. В соответствии с принятой договоренностью данная точка обозначается как 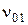. Аналогично, первый положительный максимум функции 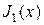приходится на значение аргумента 1,841, которое должно быть обозначено как .

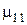Рисунок 30 − Функции Бесселя

Теперь можно вновь вернуться к исследованию воли электрического типа. В соответствии с методом разделения переменных амплитуда продольной составляющей напряженности электрического поля запишется в виде

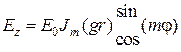
Здесь поперечное волновое число 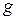пока еще не определено. Чтобы найти его, заметим, что граничное условие

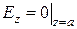
будет выполнено в том случае, если числа принадлежат бесконечной дискретной последовательности, удовлетворяющей соотношению

,

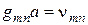откуда

.

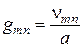Номер корня 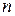является вторым индексом волны 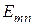. Итак, окончательно комплексная амплитуда составляющей 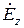для колебания типа 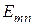принимает вид:

Физический смысл индексов 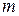и 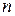очень прост: 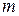означает число вариаций поля по угловой координате 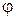, а 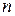— число вариаций по радиальной координате 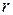. В частном случае 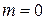поля по углу 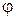не изменяются, и такие типы волн называют симметричными.

Критические длины волн находятся на основании того же самого принципа, что и в случае прямоугольного волновода:

.

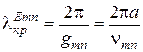Формулы для вычисления длины волны в волноводе и фазовой скорости имеют ту же структуру, что и в теории прямоугольного волновода:

,

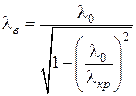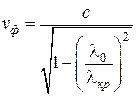
Поперечные составляющие полей для любой волны типа 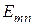легко находятся из выражения для продольной составляющей 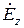и формул перехода. Покажем это на примере часто употребляемой простейшей симметричной волны типа 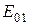. Здесь

Картина распределения полей в волноводе, построенная по этим формулам, показана на рисунке. Интересно отметить, что данная структура поля может быть получена непрерывной деформацией структуры типа 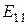в прямоугольном волноводе.

Рисунок 31 − Картина силовых линий волны типа 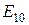в круглом волноводе