Линии передачи с волнами ТЕМ

Раньше, при классификации волн в линиях передачи, было указано на существование особого класса решений уравнений Максвелла, для которых характерно отсутствие продольных составляющих как электрического, так и магнитного векторов. Волны подобного вида при ято называть поперечными электромагнитными волнами или, сокращенно, ТЕМ-волнами.

Простейшим примербм волны типа ТЕМ может служить переменное электромагнитное поле, образующееся в волноводе из двух проводящих плоскостей при распопстранении плоской электромагнитной волны, имеющей параллельную поляризацию и падающей под углом 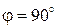(рисунок 33). Обращает на себя внимание тот факт, что данное поле по своей конфигурации полностью совпадает с однородной плоской волной: роль идеально проводящих стенок сводится лишь к локализации поля в пространстве.

Рисунок 33 − Волна типа ТЕМ в пространстве между двумя проводящими плоскостями

Отметим некоторые основные свойства волн типа ТЕМ.

1. Поскольку граничные условия для вектора 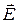в изображенной линии передачи удовлетворяются автоматически, структура поля не зависит от расстояния между плоскостями и от длины волны. Следовательно

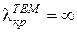
т. е. система пропускает колебания всех частот вплоть до постоянного тока.

2. Механизм распространения волны типа ТЕМ не связан с явлениями многократных отражений от стенок. Поэтому

.

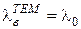Здесь под 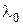в общем случае следует понимать длину однородной плоской волны в заполняющем диэлектрике.

3. Характеристическое сопротивление волны типа ТЕМ, обозначаемое как 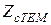и равное отношению амплитуды электрического поля к амплитуде магнитного поля, совпадает с аналогичной величиной, вычисленной для однородной плоской волны в неограниченном пространстве. Действительно,

.

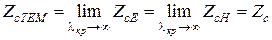В круглом и прямоугольном волноводах волны типа ТЕМ не могут существовать. Это утверждение можно обосновать так: предположим, что в волноводе распространяется волна, у которой векторы 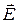и лежат в поперечной плоскости. Силовые линии вектора , являясь замкнутыми, должны охватывать линии тока. Но токи проводимости отсутствуют, поскольку внутри волновода проводников нет. Значит, током может быть только продольный ток смещения. Поэтому должна иметься продольная составляющая вектора 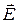, т.к. 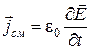. Следовательно, ТЕМ-волна (волна без продольной составляющей вектора 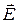) в волноводе не может распространяться. Из этих рассуждений ясно, что для существования ТЕМ-волны в замкнутой направляющей системе необходимо, чтобы последняя состояла не менее чем из двух изолированных друг от друга проводников, по которым может протекать ток проводимости. Этому условию удовлетворяют следующие линии:

1. Коаксиальная;

2. Двух- и многопроводная;

3. Полосковая.