Постановка задачи

Круглый металлический волновод представляет собой полую металлическую трубу с внутренним радиусом 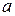, бесконечно протяженную вдоль оси 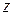(рисунок 28). Исходные предпосылки в рассматриваемом случае остаются теми же, что и при исследовании прямоугольного волновода. Так, предполагается, что проводимость стенок волновода бесконечно велика, волновод однороден по оси 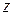и внутренней средой является вакуум. Требуется проанализировать распространение волн элктрического и магнитного типов в подобной системе.

Вообще говоря, для решения поставленной задачи можно было бы воспользоваться теми результатами, которые получены применительно к волноводу с прямоугольной формой сечения. Например, хорошо известна структура поля волны типа 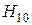в прямоугольном волноводе. Прямоугольный контур сечения может быть преобразован в круглый путем последовательных деформаций. На рис. 29 изображен один из первоначальных моментов такой деформации.

Рисунок 28 − Круглый волновод

Принципиально важно отметить, что силовые линии электрического вектора всегда должны подходить к металлическим стенкам волновода по направлению нормали. Этот принцип является определяющим при построении структуры поля. В конечном итоге получим картину, изображенную на рисунке 29. Естественно, что она соответствует основной волне круглого волновода, что и будет показано в дальнейшем

Рисунок 29 − Последовательные этапы деформации прямоугольного волновода

Несмотря на кажущуюся простоту, метод непрерывной деформации сечения мало пригоден для поставленной цели, поскольку получение числовых характеристик сопряжено здесь с весьма значительными математическими трудностями. Поэтому дальнейшее исследование будет опираться на непосредственное решение уравнений Максвелла в той системе координат, которая в наибольшей степени отвечает геометрии данного волновода.

Легко видеть, что стенки изучаемого волновода совпадают с координатной поверхностью 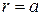цилиндрической системы координат 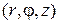. По этой причине данная система координат оказывается самой подходящей для решения поставленных задач. Уравнения Максвелла без сторонних источников:

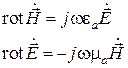
в цилиндрической системе координат принимают следующий вид:

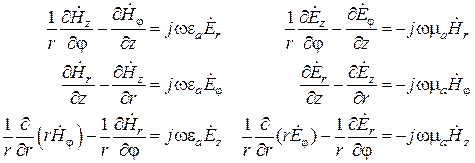
В случае направляемых волн, распространяющихся по оси 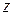, комплексные амплитуды напряженностей электрического и магнитного полей запишутся в виде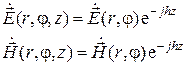

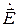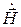Частный вид этих зависимостей позволяет, как это было сделано ранее, выразить поперечные составляющие полей и через частные производные от продольных составляющих и получить следующие формулы перехода:

.

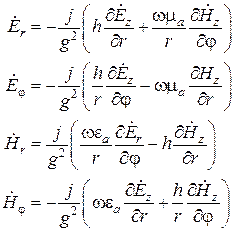Отсюда сразу вытекает возможность существования в круглом волноводе колебаний типв Е и Н в отдельности. Для их исследования необходмо решить уравнения Гельмгольца для 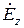и :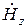

,

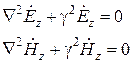которые в цилиндрической системе координат принимают вид

.

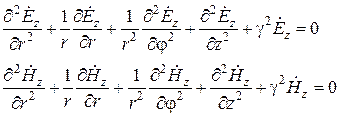Здесь использовано выражение оператора Лапласа в системе координат 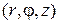. Для случая направляемых волн в последних уравнениях можно избавиться от частных производных по продольной координате, введя поперечное волновое число 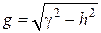. В результате получим уравнения

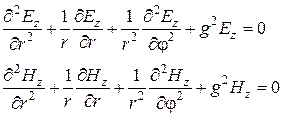
Разумеется, что однозначное решение этих уравнений возможно лишь том случае, когда они дополнены соответствующими граничными условиями на стенках волновода.