Волны типа Н в круглом волноводе
При исследовании колебаний магнитного типа нужно опираться на уравнение Гельмгольца для составляющей 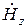 :
:
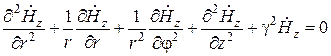
Разыскивая решение этого уравнения в виде
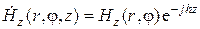
и вводя поперечное волновое число
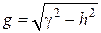 ,
,
приходим к уравнению
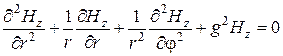
В случае волн 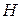 -типа электрическое поле имеет только поперечные составляющие, из которых только составляющая
-типа электрическое поле имеет только поперечные составляющие, из которых только составляющая 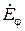 касательна к стенке волновода. Поскольку
касательна к стенке волновода. Поскольку
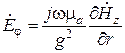 ,
,
граничные условия принимают вид
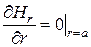 .
.
Таким образом, исследование распространения волн магнитного типа в круглом металлическом волноводе сводится к решению однородной краевой задачи Неймана для уравнения Гельмгольца.
Данная задача решается методом разделения переменных. Как и в случае волн 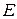 -типа, частное решение, имеющее
-типа, частное решение, имеющее 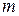 вариаций по углу
вариаций по углу 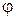 , запишется в виде
, запишется в виде
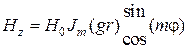
Для нахождения неизвестного поперечного волнового числа вычислим частную производную
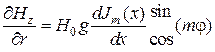
Граничные условия будут тождественно выполнены, если 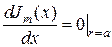 . Это равенство, рассматриваемое как уравнение относительно
. Это равенство, рассматриваемое как уравнение относительно 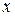 , имеет бесконечное число корней, обозначаемых здесь как
, имеет бесконечное число корней, обозначаемых здесь как 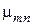 . Таким образом, краевая задача, описывающая распространение волн магнитного типа, имеет бесконечное множество нетривиальных решений, причем для каждого из этих решений
. Таким образом, краевая задача, описывающая распространение волн магнитного типа, имеет бесконечное множество нетривиальных решений, причем для каждого из этих решений 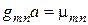 , т.е.
, т.е. 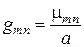 .
.
Итак, продольная составляющая магнитного поля для колебания типа 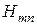 в круглом волноводе принимает вид
в круглом волноводе принимает вид
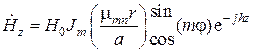 .
.
Основные расчетные формулы остаются теми же, что и для волн электрического типа:
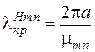 ,
,
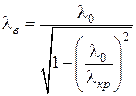 ,
, 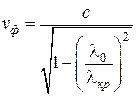 .
.
Поперечные составляющие полей для волн магнитного типа находятся на основании формул перехода. Так, например, для часто используемой волны типа 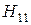 имеем:
имеем:
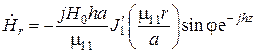 ,
,
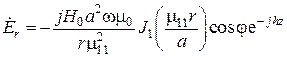 ,
,
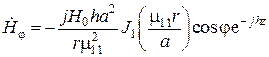 ,
,
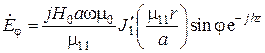 ,
,
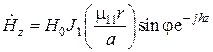 ,
, 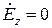 .
.
Картина поля, построенная на основании этих соотношений, показана на рисунке. Она полностью совпадает с той, которая была получена путем непрерывной деформации прямоугольного волновода с волной типа 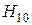 .
.

Рисунок 32 − Картина силовых линий электромагнитного поля волны типа 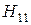 в круглом волноводе
в круглом волноводе
Большой интерес представляет также колебание 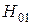 − простейшая симметричная магнитная волна в круглом волноводе. Составляющие поля для волны этого типа имеют следующий вид:
− простейшая симметричная магнитная волна в круглом волноводе. Составляющие поля для волны этого типа имеют следующий вид:
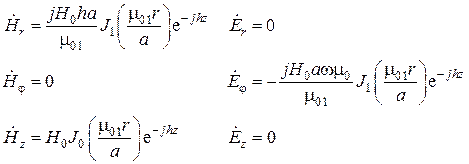
Дата добавления: 2015-10-19; просмотров: 1750;
