Волны в упругих средах

Фазовая скорость распространения механических волн зависит от макроскопических свойств среды, таких, как плотность и упругость.

Рассмотрим распространение механической волны в круглом стержне диаметром D, при условии, что D/λ < 1. Пусть импульс внешней силы FΔt вызывает деформацию сжатия (рис.6.1) размером Δx и за время Δt деформация распространится в стержне на длину

Δl = υ Δt. (6.10)

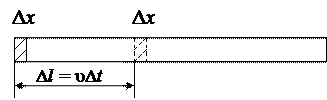
Рис.6.1

Масса сдвинутого вещества составит

Δm = Sρυ Δt, (6.11)

где S - площадь сечения стержня, ρ - плотность материала стержня.

По закону Гука

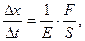(6.12)

где Е - модуль упругости или модуль Юнга.

Выразим Δm из формулы

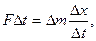(6.13)

где 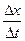- скорость деформации, и, подставив в формулу (6.12), получим

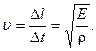(6.14)

Мы получили связь фазовой скорости с модулем объемной упругости Е для продольных волн.

Скорость поперечных волн будет

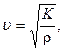(6.15)

где К - модуль сдвига.

Если в (6.14) подставить модуль упругости и плотность для газа, то найдем скорость волны в газе. Считая, что относительное изменение объема ΔV/V равнозначно относительному удлинению Δl/l, а уменьшение давления (-Δp), вызванное изменением объема, - напряжению F/S, получим для модуля упругости в газе:

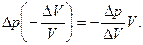(6.16)

Подставим (6.16) в (6.14) и получим:

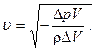(6.17)

Принимая ρ = 1/V₀ (для простоты m = 1кг), скорость волны будет:

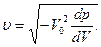(6.18)

Сжатие и разрежение газа происходит весьма быстро (адиабатно) и можно использовать уравнение Пуассона ( 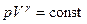). Тогда из уравнения Пуассона можно записать:

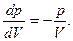(6.19)

Воспользуемся (6.19) и уравнением Клапейрона-Менделеева 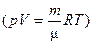для m = 1 кг. Получим:

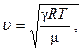(6.20)

где γ - коэффициент Пуассона;

R - универсальная газовая постоянная;

T - абсолютная температура;

μ - молярная масса.

Полученные формулы (6.14), (6.15) и (6.20) устанавливают связь между скоростью волны, механическими и химическими свойствами и температурным режимом среды. Поэтому с помощью распространяющейся волны можно решать многие задачи по изучению свойств и параметров сред в разных фазовых состояниях, которые используются в технике, строительстве и жизни.