Волновое сопротивление
Зная комплексные амплитуды электрического и магнитного полей в коаксиальной линии передачи, можно вычислить мощность электромагнитного поля, переносимую вдоль оси 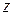 :
:
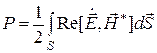
Подставляя сюда выражения для комплексных амплитуд поля и проводя интегрирование, получаем
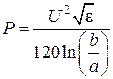 , Вт
, Вт
Эту формулу можно рассматривать как выражение для мощности, выделяемой на некотором резисторе 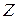 при подаче на него синусоидального напряжения
при подаче на него синусоидального напряжения 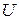 . Поскольку
. Поскольку 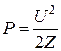 , можно записать
, можно записать
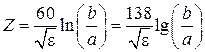 .
.
Величина 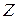 носит название волнового сопротивления коаксиальной линии передачи и имеет большое значение при решении вопросов ее реализации. Это объясняется тем, что часто используют последовательное включение линий передачи, обладающих различающимися параметрами, например, диаметрами проводников. Естественным требованием, предъявляемым к стыку двух линий, является согласование, т. е. отсутствие отражений от данной сосредоточенной неоднородности. Поскольку в плоскости стыка напряжение
носит название волнового сопротивления коаксиальной линии передачи и имеет большое значение при решении вопросов ее реализации. Это объясняется тем, что часто используют последовательное включение линий передачи, обладающих различающимися параметрами, например, диаметрами проводников. Естественным требованием, предъявляемым к стыку двух линий, является согласование, т. е. отсутствие отражений от данной сосредоточенной неоднородности. Поскольку в плоскости стыка напряжение 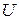 есть непрерывная функция координаты
есть непрерывная функция координаты 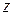 , мощность может быть целиком передана из одной линии в другую лишь при условии согласования:
, мощность может быть целиком передана из одной линии в другую лишь при условии согласования:

Данная формула во многих случаях служит критерием согласования с достаточной для инженерных целей точностью. Приближенность ее заключается в том, что здесь не учитывается изменения структуры поля в непосредственной близости от плоскости скачка геометрических размеров, происходящее за счет возбуждения нераспространяющихся колебаний высших типов.
Возможность использования понятия волнового сопротивления для линий передачи с волнами ТЕМ объясняется тем, что здесь напряжение 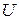 , в отличие от волноводов, может быть введено однозначным образом. Поэтому волновое сопротивление полностью характеризуется геометрическими параметрами поперечного сечения, а также диэлектрической проницаемостью использованного материала.
, в отличие от волноводов, может быть введено однозначным образом. Поэтому волновое сопротивление полностью характеризуется геометрическими параметрами поперечного сечения, а также диэлектрической проницаемостью использованного материала.
Отметим также, что волновое сопротивление линии можно выразить через ее погонную емкость. В случае ТЕМ-волны в любой однородной идеальной линии текут только продольные поверхностные токи. Их плотность 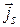 связана с плотностью поверхностных зарядов уравнением непрерывности
связана с плотностью поверхностных зарядов уравнением непрерывности
 ,
,
которое можно записать в виде
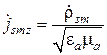 .
.
Интегрируя последнее равенство по контуру поперечного сечения проводника, по которому течет рассматриваемый ток, получим
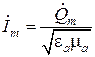 ,
,
где 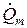 − комплексная амплитуда заряда на единицу длины проводника. Учитывая общее выражение для волнового сопротивления и определение понятия емкости конденсатора
− комплексная амплитуда заряда на единицу длины проводника. Учитывая общее выражение для волнового сопротивления и определение понятия емкости конденсатора 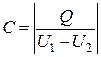 , получим
, получим
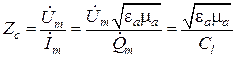 ,
,
где  − погонная емкость линии. В случае коаксиальной линии
− погонная емкость линии. В случае коаксиальной линии  определяется выражением для емкости цилиндрического конденсатора, которое получается при рассмотрении задач электростатики в курсе общей физики:
определяется выражением для емкости цилиндрического конденсатора, которое получается при рассмотрении задач электростатики в курсе общей физики:
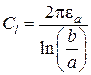
где 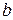 и
и 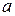 − радиусы внешней и внутренней обкладок соответственно. Подставляя это равенство в предыдущую формулу для волнового сопротивления, получим выражение для волнового сопротивления коаксиальной линии, аналогичное выведенному выше:
− радиусы внешней и внутренней обкладок соответственно. Подставляя это равенство в предыдущую формулу для волнового сопротивления, получим выражение для волнового сопротивления коаксиальной линии, аналогичное выведенному выше:
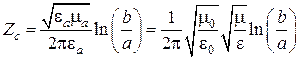 ,
,
так как 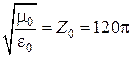 (характеристическое сопротивление свободного пространства), а
(характеристическое сопротивление свободного пространства), а 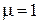 , то
, то
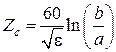 .
.
Дата добавления: 2015-10-19; просмотров: 2779;
