Падение плоской электромагнитной волны на диэлектрическое полупространство под произвольным углом
Рассмотрим, наконец, наиболее общий случай, при котором плоская электромагнитная волна, распространяясь в среде 1, падает на границу раздела под произвольным углом 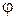 , удовлетворяющим условию
, удовлетворяющим условию 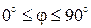 . Геометрия данной задачи и направление осей координат показаны на рисунке.
. Геометрия данной задачи и направление осей координат показаны на рисунке.
При анализе этой системы естественно выделить три волны: падающую, отраженную и преломленную. Векторы Пойнтинга всех трех перечисленных волн лежат в одной плоскости, названной плоскостью падения.
Для того, чтобы записать комплексные амплитуды электромагнитных полей, следует воспользоваться результатами рассмотрения случая распространения плоской волны в произвольном направлении, что было сделано выше.
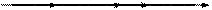
Рисунок 63 − Наклонное падение плоской волны
 .
.
Из рисунка следует, что вектор 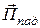 образует с положительными направлениями осей
образует с положительными направлениями осей 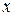 ,
, 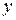 ,
, 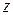 углы
углы 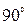 ,
, 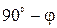 и
и 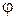 соответственно.
соответственно.
Тогда
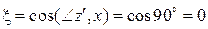 ,
,
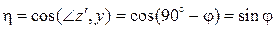 ,
,
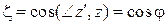 .
.
Тогда комплексная амплитуда падающей волны может быть записана следующим образом:
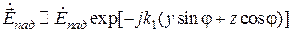
Если через 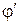 и
и 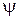 обозначить углы, указанные на рисунке и называемые соответственно углами отражения и преломления, то комплексные амплитуды отраженной и преломленной волн могут быть представлены в виде:
обозначить углы, указанные на рисунке и называемые соответственно углами отражения и преломления, то комплексные амплитуды отраженной и преломленной волн могут быть представлены в виде:
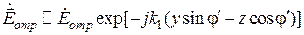 ,
,
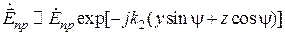
На границе раздела, т.е., в плоскости 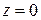 , должны выполняться условия непрерывности тангенциальных составляющих векторов
, должны выполняться условия непрерывности тангенциальных составляющих векторов 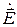 и
и 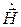 , т.е.
, т.е.
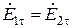 ,
, 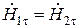 при
при 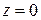 .
.
Например, для вектора напряженности электрического поля получим
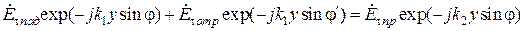
Поскольку все точки поверхности разделя являются совершенно равноправными, это соотношение должно являться тождеством относительно переменной 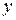 . Для этого необходимо, чтобы показатели всех экспонент, входящих в него, были равны при всех
. Для этого необходимо, чтобы показатели всех экспонент, входящих в него, были равны при всех 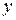 . Данное условие может быть записано в виде двух равенств:
. Данное условие может быть записано в виде двух равенств:
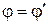 ,
,
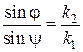 .
.
Таким образом, получены два хорошо известных из элементарной физики закона, определяющих поведение волн на границе раздела двух сред. Эти законы носят название законов Снеллиуса (Снелля) и формулируются следующим образом:
1. Угол падения равен углу отражения.
2. Отношение синусов угла падения и преломления равно обратному отношению показателей преломления.
Поскольку 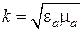 , второй закон Снеллиуса может быть записан в таком виде, что в него войдут лишь электродинамические параметры граничащих сред. Для этого для каждой среды введем величину
, второй закон Снеллиуса может быть записан в таком виде, что в него войдут лишь электродинамические параметры граничащих сред. Для этого для каждой среды введем величину 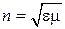 , носящую название показателя преломления данной среды. Тогда
, носящую название показателя преломления данной среды. Тогда 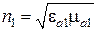 и
и 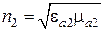 . Если, например,
. Если, например, 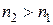 , то принято говорить, что вторая среда обладает большей оптической плотностью, чем первая. Используется также понятие относительного показателя преломления двух сред
, то принято говорить, что вторая среда обладает большей оптической плотностью, чем первая. Используется также понятие относительного показателя преломления двух сред 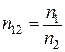 . В этом случае закон Снеллиуса примет вид
. В этом случае закон Снеллиуса примет вид
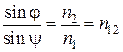 .
.
Рассмотренные закономерности верны безотносительно ориентации векторов поля к плоскости падения. Более тщательный анализ показывает, что в силу векторного характера электромагнитного поля ряд явлений, возникающих при падении плоской электромагнитной волны на границу раздела, существенно различается в зависимости от взаимной ориентации плоскостей поляризации и падения. Поэтому следует более подробно рассмотреть два случая.
Дата добавления: 2015-10-19; просмотров: 1198;
