Полное прохождение. Угол Брюстера

При падении плоских электромагнитных волн на границу раздела двух сред при определенных условиях коэффициент отражения может обратиться в нуль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера или углом полного преломления и обозначается как .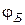

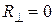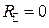Условия, при которых отсутствует отраженная волна, могут быть установлены путем решения уравнений и относительно угла падения 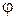. В частном случае, когда обе среды являются немагнитными диэлектриками, существование угла Брюстера легко определяется из физических соображений.

Рисунок 66 − Угол Брюстера

Пусть параллельно поляризованная волна падает на плоскую границу раздела двух немагнитных диэлектриков. Под воздействием поля преломленной волны среда поляризуется: дипольные моменты молекул второй среды ориентируются параллельно вектору напряженности электрического поля преломленной волны. Упорядоченно ориентированные молекулярные диполи второй среды излучают электромагнитные волны, суперпозиция которых и образует в первой среде плоскую отраженную волну. Молекулярный диполь (его можно считать элементарным электрическим вибратором) не излучает вдоль своей оси. Следовательно, отраженная волна не может возникнуть, если оси упорядоченно ориентированных молекулярных диполей будут параллельны направлению, в котором должна распространяться отраженная волна.

Определим теперь величину угла Брюстера. Из найденных выше уравнений для коэффициентов отражения и преломления

,

,

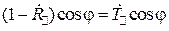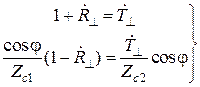следует, что угол Брюстера 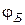удовлетворяет одному из двух уравнений:

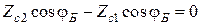
при перпендикулярной поляризации либо

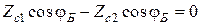
при параллельной поляризации. Здесь под 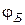подразумевается угол преломления, соответствующий углу Брюстера.

Легко видеть, что эти два уравнения взаимно протеворечат друг другу, т. е. явление полного преломления можно наблюдать либо при перпендикулярной, либо при параллельной поляризации. Рассмотрим наболее часто встречающийся случай, когда обе граничащие среды являются немагнитными 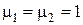и оптическая плотность второй среды больше, чем первой 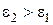. Из данных предположений следует, что

.

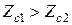Кроме того, в силу второго закона Снеллиуса 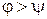, т.е.

.

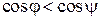Обращаясь к вышеприведенным формулам, видим, что первое из этих уравнений в рамках сделанных предположений вообще не может иметь решений. Таким образом, угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать только при параллельной поляризации.

Удобную формулу для вычисления угла Брюстера можно получить из выражения для коэффициента отражения при падении волны из вакуума на диэлектрик:

.

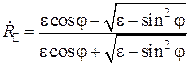Действительно, угол Брюстера должен удовлетоворять условию

,

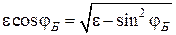откуда легко находим

.

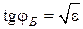Плоские волны круговой и эллиптической поляризации можно представить в виде суперпозиции двух линейно поляризованных плоских волн, одна из которых поляризована нормально, а другая − параллельно плоскости падения. Так как условия существования угла Брюстера для параллельной и нормальной поляризаций различны, то волны с круговой или эллиптической поляризацией будут отражать при любых углах падения. Однако при этом соотношение между амплитудами нормальной и параллельной составляющих в отраженной и преломленной волнах будет иным, чем в падающей волне. Это приводит к изменению поляризации отраженной и преломленной волн по сравнению с падающей. В частности, если плоская волна с круговой поляризацией падает под углом Брюстера для одной из образующих ее линейно поляризованных волн, то отраженная волна оказывается линейно поляризованной, а преломленная волна − эллиптически поляризованной.

Явление полного преломления может иметь полезные технические приложения. Так, пластинка из диэлектрика, установленная под углом Брюстера по отношению к направлению распространения падающей волны, не создает отражений. При этом эта же пластина может играть роль важного конструктивного элемента, например, обеспечивая уплотнение какого-либо прибора.