Наклонное падение на границу раздела двух сред при параллельной (вертикальной) поляризации

Здесь векторы 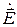во всех трех волнах параллельны плоскости падения. Можно также сказать, что вектор 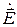имеет вертикальную поляризацию, если .

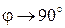Так же, как и для перпендикулярной поляризации, могут быть записаны граничные условия непрерывности тангенциальных составляющих векторов электромагнитного поля. Они принимают вид

,

.

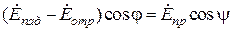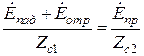Рисунок 65 − Случай параллельной поляризации

Введем коэффициенты отражения 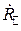и преломления 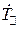по электрическому полю. Значок внизу указывает, что данные величины относятся к случаю параллельной поляризации. Поделив левые и правые части уравнений граничных условий на амплитуду падающей волны 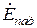, получаем следующую систему уравнений относительно 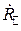и :

,

,

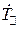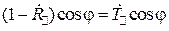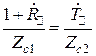откуда

,

.

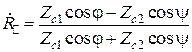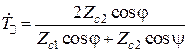Для случая, когда средой 2 является немагнитный диэлектрик с относительной проницаемостью 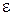, последние формулы приводятся к виду, более удобному для расчетов:

,

.

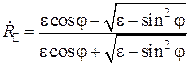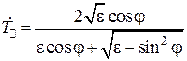Таким образом, на основании двух последних рассмотренных случаев приходим к выводу, что при различных поляризациях законы изменения коэффициентов отражения и преломления описываются разными функциями. Если рассмотреть наиболее общий случай, когда на границу раздела падает плоская электрмагнитная волна с вращающейся эллиптической поляризацией, то отсюда следует, что все три волны − падающая, отраженная и преломленная − характеризуются различными коэффициентами эллиптичности, причем коэффициенты эллиптичности отраженной и преломленной волн зависят от угла падения.