Наклонное падение на границу раздела двух сред при перпендикулярной (горизонтальной) поляризации
Этот случай характеризуется тем, что плоскость поляризации, т.е., плоскость, содержащая вектор 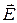 , перпендикулярна плоскости падения (рисунок 64). Другими словами, вектор
, перпендикулярна плоскости падения (рисунок 64). Другими словами, вектор 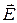 расположен горизонтально по отношению к плоскости раздела сред.
расположен горизонтально по отношению к плоскости раздела сред.
Рисунок 64 − Случай перпендикулярной поляризации
Определять коэффициенты отражения и преломления для случая перпендикулярной (горизонтальной) поляризации будем, пользуясь принципом непрерывности тангенциальных составляющих поля на границе раздела.
Граничные условия относительно напряженности электрического поля запишутся весьма просто:
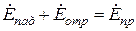 .
.
При записи граничных условий относительно векторов напряженности магнитного поля следует учесть, прежде всего, что тангенциальные составляющие получаются за счет умножения модулей векторов 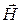 на косинусы соответствующих углов. Кроме того, в данной задаче весьма удобно выразить выекторы
на косинусы соответствующих углов. Кроме того, в данной задаче весьма удобно выразить выекторы 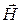 через векторы
через векторы 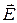 , пользуясь понятием характеристических сопротивлений сред. Таким образом, условие непрерывности тангенциальных составляющих векторов
, пользуясь понятием характеристических сопротивлений сред. Таким образом, условие непрерывности тангенциальных составляющих векторов 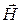 в плоскости
в плоскости 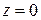 примет вид
примет вид
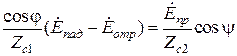 .
.
Введем коэффициенты отражения и преломления по нулю, указав значком снизу, что эти величины относятся к случаю перпендикулярной поляризации:
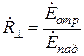 ,
, 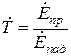 .
.
Теперь, граничное условие и второй закон Снеллиуса можно объединить, получив систему двух алгебраических линеныйх уравнений относительно 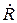 и
и 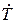 :
:
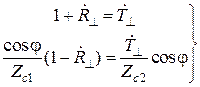
Решение этой системы имеет вид
косинус пси
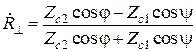 ,
,
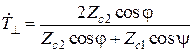 .
.
Интересно отметить, что вид этих соотношений аналогичен виду формул, полученных для случая нормального падения плоской волны на диэлектричское полупространство. Отличие состоит лишь в том, что здесь характеристические сопротивления приходится умножить на косинусы соответствующих углов. При пользовании данными формулами необходимо, задаваясь некоторым значением угла падения 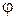 , одновременно вычислить угол преломления
, одновременно вычислить угол преломления 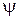 на основании первого закона Снеллиуса.
на основании первого закона Снеллиуса.
На практике весьма часто приходится вычислять характеристики отражения и преломления для частного случая, когда средой 1 является вакуум или воздух ( 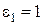 ,
, 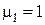 ), а средой 2 − немагнитный (
), а средой 2 − немагнитный ( 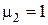 ) диэлектрик с относительной проницаемостью
) диэлектрик с относительной проницаемостью 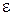 . При этом удается объединить формулы со вторым законом Снеллиуса и записать их в виде
. При этом удается объединить формулы со вторым законом Снеллиуса и записать их в виде
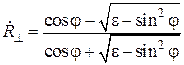 ,
,
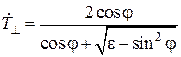 .
.
Дата добавления: 2015-10-19; просмотров: 1163;
