Нормальное падение электромагнитной волны на идеально проводящую плоскость

Рассмотрим следующую идеализированную задачу. Пусть на идеально проводящую бесконечную плоскость по направлению нормали падает плоская электромагнитная волна, распространяющаяся вдоль оси 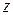декартовой системы координат (рисунок 61).

Рисунок 61 − Падение плоской волны на идеально проводящую плоскость

Из рисунка видно, что присутствие на поверхности идеального металла лишь вектора напряженности электрического поля падающей волны 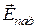не может обеспечить выполнение граничного условия 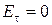. Для того, чтобы данное условие выполнялось, необходимо допустить наличие в полупространстве 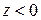отраженной волны, причем при 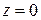справедливо равенство

.

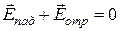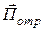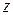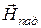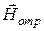Для того, чтобы определить суммарное магнитное поле, существующее на поверхности идеального металла, следует учитывать, что вектор Пойнтинга отраженной волны направлен в отрицательном направлении вдоль оси . Поскольку модули векторов и равны между собой 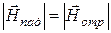, модуль суммарного вектора

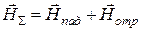
в два раза больше, чем модуль каждого из слагаемых. Таким образом, получатся весьма важный результат − на поверхности идеального проводника суммарное магнитное поле удваивается по сравнению с магнитным полем падающей волны:

.

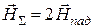Знание величины и направления суммарного магнитного поля позволяет определить вектор плотности поверхностного тока по формуле

.

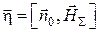Из рисунка видно, что поверхностный ток протекает в направлении вектора 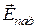, а его амплитуда равна удвоенной амплитуде магнитного поля падающей волны.