Необходимое число измерений для оценки среднеквадратического

отклонения с точностью 50 %

Под точностью оценки среднеквадратического отклонения 50 % (0.5 – в долях от единицы) понимается величина относительной точности , где L – ширина доверительного интервала.

Определение необходимого числа измерений может быть произведено с помощью неравенства , полученного из интервальной оценки для генеральной дисперсии (2.21). Поскольку в это выражение не входят числовые характеристики распределения конкретной случайной величины, то для достижения одинаковой точности оценки e в обоих случаях (и для новой и для старой технологий) потребуется проделать одинаковое число опытов, которое можно определить из неравенства .

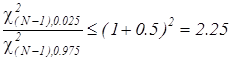Решение этого неравенства также может быть произведено численным методом – методом подбора, с использованием таблиц квантилей распределения Пирсона (табл. П.3), как это показано в табл. 3.3. Процедура расчета следующая: 1) выбираем некоторое значение объема выборки N; 2) по табл. П.3 определяем значения квантиле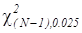й и ; 3) рассчитываем их отношение и сравниваем результат со значением . Если значение отношения квантилей оказалось больше чем 2.25, то принимаем новое, большее значение N. При этом, из соображений экономии затрат на проведение эксперимента, следует подобрать минимально допустимое число измерений N.

Таблица 3.3

Расчет необходимого числа измерений для оценки стандартного

отклонения с точностью 0.5

Число измерений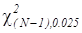
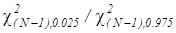
	11.14	0.48	23.00
	19.02	2.70	7.04
	32.85	8.91	3.69
	45.72	16.05	2.85
	58.12	23.65	2.46
	70.22	31.55	2.23
	64.20	27.57	2.33
	65.41	28.37	2.31
	66.62	29.16	2.28
	67.82	29.96	2.26
	69.02	30.75	2.24

Вывод: Для того чтобы оценить математическое ожидание диаметра катанки с точностью 0.1 мм, необходимо произвести 13 измерений для старой технологии и 17 измерений для новой. Для нахождения оценки стандартного отклонения диаметра с точностью 0.5 необходимо произвести 49 измерений.