Распределения

Учитывая, что объем опытных данных, составляющих выборки, очень мал, применение строгих параметрических или общих критериев согласия нецелесообразно в связи с их малой мощностью. Поэтому проверку согласия распределения случайной величины диаметра катанки нормальному закону распределения произведем при помощи приближенного критерия – критерия среднего абсолютного отклонения, пригодного для анализа выборок малого объема. Статистикой этого критерия является величина 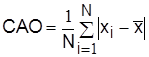. Значения сумм подсчитаны в табл. 3.2.

Эмпирический закон распределения с вероятностью 95 % не противоречит теоретическому нормальному закону распределения, если выполняется неравенство :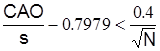

а) для первой выборки (старая технология) .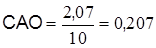

Поскольку 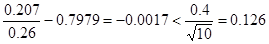, то эта выборка не противоречит нормальному закону распределения;

б) для второй выборки (новая технология) .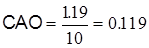

Поскольку 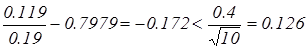, то и вторая выборка также не противоречит нормальному закону распределения.

Вывод: Выборки результатов измерений диаметров катанки, полученные для старой и новой технологий с вероятностью 95 %, не противоречат нормальному закону распределения.