И значения диаметра, которое не будет превышено

с вероятностью 95%

По ГОСТ 2590-88 допуск на катанку с номинальным диаметром 6 мм составляет 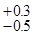мм, т.е. диапазоном возможных изменений диаметра катанки является 5.5...6.3 мм.

Проведем нормирование границ оцениваемого интервала:

а) для старой технологии известно генеральное значение среднеквадратического отклонения σ_c=0.18 мм. Поскольку генеральное значение более точное, чем оценка (выборочное среднеквадратическое отклонение s_c), то при проведении нормирования целесообразнее использовать именно σ_c:

левая граница ;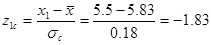

правая граница ;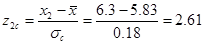

б) для новой технологии генеральное значение среднеквадратического отклонения σ_н не известно, поэтому используем выборочное значение s_н:

левая граница ;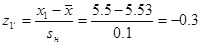

правая граница .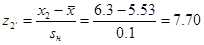

Для определения вероятности попадания диаметра катанки в поле допусков воспользуемся функцией Лапласа Ф(z) (табл. П.1):

а) для старой технологии:

P(5.5<X_C£6.3)=P(-1.83<Z_C£2.61)=Ф(2.61)-Ф(-1.83)= Ф(2.61)-(1-Ф(1.83))=

=0.9955-(1-0.9664)=0.9619;

б) для новой технологии:

P(5.5<X_Н£6.3)=P(-0.3<Z_Н£7.7)=Ф(7.7)-Ф(-0.3)= Ф(7.7)-(1-Ф(0.3))=

=1-(1-0.6179)= 0.6179.

При расчете принято, что Ф(7.7)≈1.

Расчет значения, которое не будет превышено с вероятностью 95 %

Значение диаметра катанки, которое не будет превышено с вероятностью 95 % по сути своей является квантилью случайной величиной диаметра катанки порядка 0.95. Рассчитать такое значение наиболее просто можно используя нормированное нормальное распределение (табл. П.2).

Из условия нормирования (2.10) можно получить выражение для расчета нормально распределенной величины Хпри известном значении нормированной нормально распределенной величины Z: 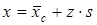. Если под х понимается значение квантили порядка 0.95, то и z будет квантилью того же порядка.

Для доверительной вероятности 0.95 табличное значение квантили z_0.95=1.645 (табл. П.2);

а) для старой технологии известно генеральное значение среднеквадратического отклонения σ_c=0.18 мм. Используем его:

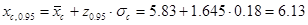мм;

б) для новой технологии:

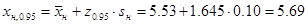мм.

Анализируя полученные результаты расчетов, можно отметить следующее:

1) для старой технологии вероятность попадания диаметра катанки в поле допусков составляет 96.19 %, что говорит о недостаточно высокой устойчивости процесса прокатки, так как вероятность получения катанки вне поля допуска по диаметру весьма высока (100-96.19=3.81 %). Необходим поиск путей совершенствования технологии. Одним из известных путей повышения точности сортового проката и, в частности, катанки является установка ЧБК;

2) расчет вероятности получения катанки в поле допуска после установки ЧБК показал, что она стала еще меньше – 61.79 %. Это с первого взгляда кажется не логичным, однако следует учитывать стремление прокатать катанку как можно меньшего диаметра. В результате расчета значения диаметра, который не будет превышен с вероятностью 95 %, установлено, что таковым для прокатки с применением ЧБК является значение 5.69 мм. По ГОСТ 2590-88 значение диаметра 5.69 мм входит также и в поле допусков диаметра катанки более мелкого размера 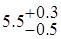мм.

Рассчитаем вероятность попадания диаметра катанки произведенной по новой технологии, в поле допуска номинального диаметра 5.5 мм, то есть в диапазон величин от 5.0 до 5.8 мм.

Проведем нормирование границ рассматриваемого интервала диаметров:

; .

Воспользовавшись функцией Лапласа (табл. П.1) получим

P(5.0<X_Н£5.8)=P(-5.3<Z_Н£2.7)=Ф(2.7)-Ф(-5.3)= Ф(2.7)-(1-Ф(5.3))=

=0.9965-(1-1)= 0.9965.

Вывод: Вероятность попадания диаметра катанки, производимой по старой технологии, в поле допуска по ГОСТ 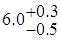мм составляет 96.19 %, при этом с вероятностью 95 % не превышается значение диаметра 6.17 мм.

Проведенный анализ позволяет высказать предположение о том, что после установки ЧБК целесообразно перейти на производство катанки с номинальным диаметром 5.5 мм. При этом вероятность попадания диаметра катанки в поле допуска по ГОСТ 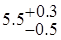мм составляет 99.65 %, и с вероятностью 95 % не будет превышено значение диаметра 5.69 мм.

Предположение о целесообразности перехода на производство катанки меньшего диаметра после установки ЧБК является именно предположением, так как весь расчет основан на использовании случайных значений среднего арифметического и выборочного среднеквадратического отклонения диаметра, причем рассчитанных по выборке весьма малого объема. Для получения объективных, обоснованных выводов необходимо использовать объективные, детерминированные показатели, такие как математическое ожидание и генеральная дисперсия (или генеральное среднеквадратическое отклонение).