Проверка выборок на наличие резко выделяющихся, инородных значений
Проверку проведем с помощью стандартного алгоритма проверки статистических гипотез, описанного в п.2.2, и критериев, приведенных в табл. 2.1:
а) для старой технологии
Из табл. 3.2 видно, что наибольшее абсолютное отклонение от выборочного среднего арифметического для старой технологии 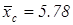 мм имеет второе значение диаметра х2=5.30 мм:
мм имеет второе значение диаметра х2=5.30 мм: 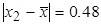 мм. Именно это значение следует проверить в первую очередь на принадлежность генеральной совокупности диаметров катанки, получаемых по старой технологии Хс:
мм. Именно это значение следует проверить в первую очередь на принадлежность генеральной совокупности диаметров катанки, получаемых по старой технологии Хс:
1) Н0: х2=5.30ÎХс – гипотеза о принадлежности значения х2 генеральной совокупности Хс эквивалентна гипотезе о том, что значение х2 не является резко выделяющимся;
2) Н1: х2=5.30ÏХ – гипотеза о том, что значение х2 является инородным;
3) поскольку для старой технологии известно генеральное среднеквадратическое отклонение диаметра катанки (s=0.18 мм), то в качестве статистического критерия следует использовать t-критерий (см. табл. 2.1);
4) t-статистика:  ;
;
5) из табл. П.7 для уровня значимости a=0.05 и числа опытных данных N=10 находим границу критической области ta,N=t0.05,10=2.44.
Для установления местоположения критической области относительно границы (слева или справа) используем метод пробной точки. Подберем такое пробное значение диаметра катанки хпр , про которое со 100 %-ной уверенностью можно сказать, что оно не является инородным, т. е. что со 100%-ной вероятностью справедлива нулевая гипотеза. В качестве такового значения можно использовать, например, среднее арифметическое хпр= 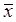 . Если подставить
. Если подставить 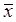 вместо хi в формулу для расчета t-статистики, то получим, что t=0. Поскольку значение t=0 располагается на числовой оси значений t слева от границы критической области ta,N, то и область принятия нулевой гипотезы также располагается слева от границы, а критическая область – справа.
вместо хi в формулу для расчета t-статистики, то получим, что t=0. Поскольку значение t=0 располагается на числовой оси значений t слева от границы критической области ta,N, то и область принятия нулевой гипотезы также располагается слева от границы, а критическая область – справа.
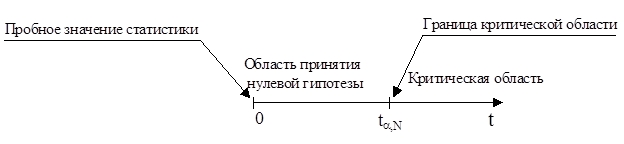
6) поскольку t=2.667>ta,N=2.44, то t-статистика попала в критическую область. Это дает основания отвергнуть нулевую гипотезу и принять альтернативную, говорящую о том, что проверяемое значение х2=5.30 является резко выделяющимся. Значение х2 следует отбросить и при дальнейших рассуждениях не учитывать;
б) для новой технологии
Из табл. 3.2 следует, что проверить на принадлежность генеральной совокупности Хн в первую очередь следует пятое значение х5=5.01 мм. Оно имеет наибольшее абсолютное отклонение от выборочного среднего 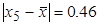 мм:
мм:
1) Н0: х5=5.01ÎХн;
2) Н1: х5=5.01ÏХн;
3) поскольку для новой технологии генеральное среднеквадратическое отклонение не известно, то для проверки следует использовать критерий Н.В. Смирнова (см. табл. 2.1);
4) u-статистика: 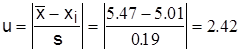 ;
;
5) из табл. П.7 для уровня значимости a=0.05 и числа опытных данных N=10 находим ua,N=u0.05,10=2.18. Местоположение критической области определяется аналогично тому, как это сделано в п. а). Критическая область также располагается справа от границы;
6) поскольку u=2.42>ua,N=2.18, то u-статистика попала в критическую область. Это говорит о том, что значение 5.01 является резко выделяющимся, его не следует учитывать при дальнейших расчетах.
Выявленные резко выделяющиеся значения (которые могут быть ошибками измерений, ошибками записи, следствием нарушения технологии прокатки и т.п.) следует отбросить из массивов опытных данных и рассчитать новые точечные оценки числовых параметров распределения, как это сделано в п. 3.1. Расчет опущен, его результаты приведены в табл. 3.4.
Таблица 3.4
Точечные оценки распределения диаметра катанки
после исключения резко выделяющихся значений
| Технология | Среднее арифметическое, мм | Выборочная дисперсия, мм2 | Среднеквадратическое отклонение, мм |
| Старая | 5,83 | 0,0428 | 0,21 |
| Новая | 5,53 | 0,0108 | 0,10 |
Для урезанных (цензурированных) выборок вновь следует выявить подозрительные значения и проверить их на принадлежность генеральной совокупности, как это проделано выше. Результаты такого расчета приведены в табл. 3.5.
Таблица 3.5
Результаты расчетов при проверке выборок на наличие
резко выделяющихся значений (второй расчет)
| Старая технология (первый массив) | Новая технология (второй массив) | ||||||
| Проверяемое значение | t-стати- cтика | ta,N | Проверяемое значение | u-стати- стика | ua,N | ||
| Номер | Величина | Номер | Величина | ||||
| 5.46 | 2.08 | 2.39 | 5.74 | 2.06 | 2.11 |
Из табл. 3.5 видно, что условия t£ta,N и u£ua,N выполняются. Это говорит о попадании статистики в область принятия нулевой гипотезы, что в свою очередь подтверждает принадлежность рассматриваемых значений соответствующим генеральным совокупностям диаметров.
Вывод: Исходные массивы данных содержали по одному резко выделяющемуся значению (2-е значение для старой технологии и 5-е значение для новой технологии), которые отброшены и в дальнейших расчетах учитываться не будут.
Дата добавления: 2015-10-13; просмотров: 1594;
