Ожидания с точностью 0.1 мм

Для определения необходимого числа измеренийиспользуем выражения, применяемые для расчета интервальной оценки математического ожидания:

а) для старой технологии известно генеральное среднеквадратическое отклонение, поэтому для расчета необходимого количества измерений N можно воспользоваться выражением (2.19). После несложных преобразований можно получить следующее уравнение: .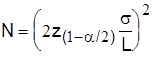

Подставив L=2×0.1=0.2 мм, s_с=0.18 мм и значение квантили нормированного нормального закона распределения из табл. П.2 z_(1-a/2)=z_0.975=1.96, получим 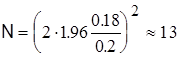измерений;

б) для новой технологии известно только выборочное среднеквадратическое отклонение, поэтому для расчета необходимого количества измерений следует воспользоваться выражением, полученным из уравнения для соответствующего случая расчета интервальной оценки математического ожидания (2.20) .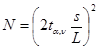

Подставив L=2×0.1=0.2 мм и s=0.19 мм, получим

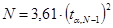. (3.1)

Поскольку значения квантилей распределения Стьюдента 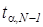(табл. П.6) зависят от количества измерений, то решить это уравнение в явном виде нельзя. Наиболее просто решение может быть получено численным методом, в данном случае – методом последовательного приближения.

Процедура расчета следующая: 1) принимаем некоторое исходное значение объема выборки N; 2) определяем по табл. П.6 значение квантили 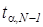; 3) по выражению (3.1) рассчитываем объем выборки N'. Если N и N' совпали, то расчет заканчиваем, если нет, то принимаем N' за N и повторяем процедуру.

Примем в качестве начального приближения N=11 измерений (выбрано произвольно). Будем округлять результаты вычислений до ближайшего целого в большую сторону:

при N=11 t_a,N-1=2.228, N’=3.62×2.228²»18;

при N=18 t_a,N-1=2.110, N’»17;

при N=17 t_a,N-1=2.120, N’»17.

Поскольку принятое значение N=17 и рассчитанное N’ совпали, то расчет закончен.