Интервальные оценки. 3.1.2.1. Интервальная оценка математического ожидания

3.1.2.1. Интервальная оценка математического ожидания

Требуется построить интервал, который с вероятностью 95 % накроет неизвестное значение математического ожидания:

а)для старой технологиигенеральная дисперсия известна, поэтому при построении доверительного интервала для математического ожиданияm_с используем выражение (2.19). Квантиль нормированного нормального распределения 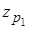для доверительной вероятности Р₁=1-a/2=1-0.05/2=0.975определяем по табл. П.2: .

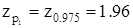Тогда ;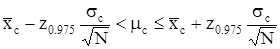

;

;

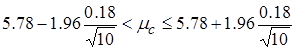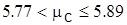б)для новой технологии генеральная дисперсия неизвестна, поэтому для построения доверительного интервала для математического ожиданияm_н используем выражение (2.20). Значение квантили t_a/2,n распределения Стьюдента для уровня значимости a/2=(1-р)/2и числа степеней свободы n=N-1 определяем по табл. П.6.

Для уровня значимости a=0,05 и числа степеней свободы n=N-1=10-1=9 табличное значение квантили составит .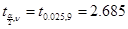

Тогда ;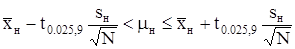

;

.

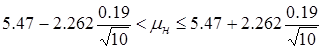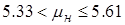3.1.2.2. Интервальная оценка генеральной дисперсии

Требуется построить интервал, который с вероятностью 95 % накроет неизвестное значение генеральной дисперсии:

а) строить интервальную оценку для генеральной дисперсии для старой технологии не имеет смысла, так как известно точное численное значение генерального среднеквадратического отклонения s_с=0.18 мм, а следовательно, можно рассчитать точное значение генеральной дисперсии s_с²=0,0324 мм²;

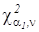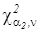б) для новой технологии интервальная оценка для генеральной дисперсии определяется выражением (2.21). Квантили распределения Пирсона и для уровней значимости α₁=a/2 и α₂=1-a/2 и чисел степеней свободы ν=N-1 определим по табл. П.3: ;

.

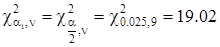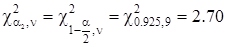Тогда ;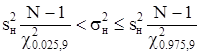

;

.

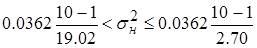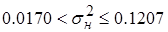Вывод: Для старой технологии среднее значение диаметра катанки составляло 5.78 мм при выборочном среднеквадратическом отклонении 0.26 мм. Для новой технологии эти показатели имеют значения 5.47 мм и 0.19 мм. Можно сделать предварительное заключение (статистическая значимость которого будет оценена ниже) о преимуществах новой технологии по сравнению со старой с точки зрения возможности получения катанки меньшего диаметра ( 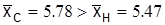) и повышения ее точности ( 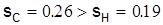). Однако, сравнивая известное генеральное (точное) значение среднеквадратического отклонения для старой технологии σ_с=0.18 мм и значение оценки среднеквадратического отклонения для новой технологии s_н=0.19 мм, можно прийти к обратному выводу с точки зрения повышения точности прокатки.