Законы распределения ДСВ
Рассмотрим некоторые законы распределения дискретной СВ.
- Биноминальное распределение
Пусть имеется 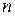 испытаний Бернулли с вероятностью успеха
испытаний Бернулли с вероятностью успеха 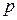 и неуспеха
и неуспеха 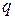 ,
, 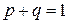 . Дискретная СВ X – число успехов имеет распределение
. Дискретная СВ X – число успехов имеет распределение
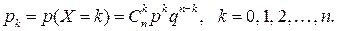
Это распределение называется биноминальным с параметрами p и q.
Математическое ожидание и дисперсия СВ X:
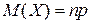 ,
,  .
.
- Геометрическое распределение
Дискретная СВ X имеет геометрическое распределение, если она принимает значения 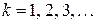 (счетное множество значений) с вероятностью
(счетное множество значений) с вероятностью
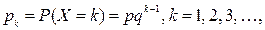
где 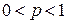 ,
, 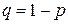
Случайная величина 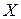 , имеющая геометрическое распределение, представляет собой число Бернулли до первого успеха.
, имеющая геометрическое распределение, представляет собой число Бернулли до первого успеха.
Математическое ожидание и дисперсия 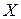 :
:
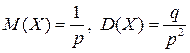 .
.
- Гипергеометрическое распределение
Дискретная СВ X имеет гипергеометрическое распределение, если она принимает значения 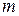 с вероятностями
с вероятностями
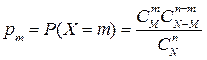
где 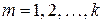 ;
; 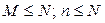 . Вероятность
. Вероятность  является вероятностью выбора
является вероятностью выбора 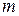 объектов, обладающих заданным свойством, из множества n объектов, случайно извлеченных (без возврата) из совокупности
объектов, обладающих заданным свойством, из множества n объектов, случайно извлеченных (без возврата) из совокупности 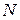 объектов, среди которых
объектов, среди которых 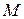 объектов обладают заданным свойством.
объектов обладают заданным свойством.
Математическое ожидание и дисперсия СВ, имеющей гипергеометрическое распределение с параметрами 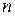 ,
, 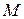 ,
, 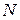 :
:
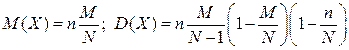 .
.
- Закон Пуассона
Говорят, что СВ X распределена по закону Пуассона, если она принимает целые значения 0, 1, 2, … с вероятностями
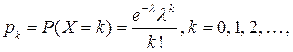
где 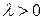 – параметр распределения,
– параметр распределения, 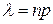 ,
, 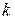 - число появления события
- число появления события 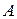 в
в 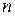 независимых испытаниях.
независимых испытаниях.
Математическое ожидание и дисперсия пуассоновской СВ равны параметру распределения:
 .
.
Закону распределения Пуассона обычно подчинена СВ, задающая простейший поток событий (число вызовов скорой помощи, число вызовов на АТС, число заказов на предприятии бытовых услуг, и т.д.) Если интенсивность потока 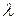 выражает число появлений события за единицу времени, то вероятность наступления
выражает число появлений события за единицу времени, то вероятность наступления 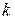 событий за время
событий за время 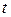 определяется формулой Пуассона
определяется формулой Пуассона 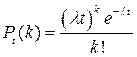 .
.
Пример 6.3. Из 25 подписчиков на газеты 16 человек подписались на местные газеты, остальные – на республиканские. Наудачу выбрали 3 подписчиков. СВ X – количество подписчиков на местные газеты среди выбранных.
Записать закон распределения СВ X. Составить функцию распределения и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Найти 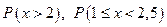 .
.
Решение. 1) Среди трех отобранных подписчиков количество человек, подписавшиеся на местные газеты может принимать следующие значения: 0, 1, 2, 3. Значит, СВ X имеет значения 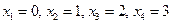 . Данная СВ X распределена по гипергеометрическому закону. Поэтому вероятности появления каждой СВ X находим по формуле:
. Данная СВ X распределена по гипергеометрическому закону. Поэтому вероятности появления каждой СВ X находим по формуле:
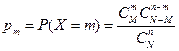 .
.
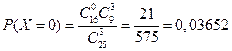 ;
; 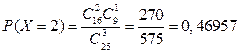 ;
;
 ;
; 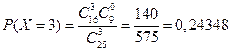 .
.
Для контроля 
+0,46957+0,24348=1.
Записываем закон распределения ДСВ X в виде таблицы:
| X | ||||
| p | 0,03652 | 0,25043 | 0,46957 | 0,24348 |
2) Данные значения СВ X разбивают числовую прямую на пять промежутков.
Если 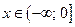 , то
, то 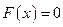 ;
;
Если 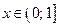 , то
, то 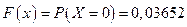 ;
;
Если 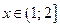 , то
, то 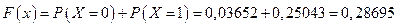 ;
;
Если 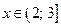 , то
, то 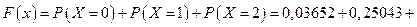
+0,46957=0,75652;
Если 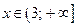 , то
, то 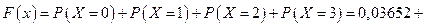
+0,25043+0,46957+0,24348=1.
Таким образом, получаем следующую функцию распределения
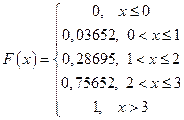 .
.
Строим график функции распределения:

3) Находим математическое ожидание СВ X:
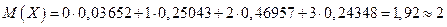 .
.
Найдем дисперсию:
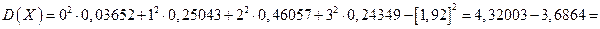
=0,63363≈0,634
Найдем среднее квадратическое отклонение:
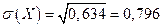 .
.
 ;
;
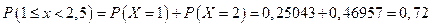 .
.
,
Дата добавления: 2015-10-09; просмотров: 4519;
