Числовые характеристики ДСВ. Можно считать, что закон распределения полностью характеризует СВ

Можно считать, что закон распределения полностью характеризует СВ. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают СВ суммарно: такие числа называют числовыми характеристиками СВ. К числу важных числовых характеристик относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана.

Определение 6.3. Математическим ожиданием ДСВ (обозначается 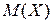)называют сумму произведения всех ее возможных значений 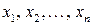на их вероятности :

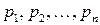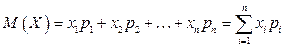. (6.2)

Замечание: Из определения следует, что математическое ожидание ДСВ есть неслучайная (постоянная) величина.

В случае счетнозначной величины, которая может принимать значения x₁, x₂, …, x_n, … с вероятностями p₁, p₂, …, p_n, …,

,

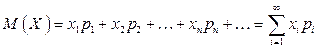где предполагается абсолютная сходимость ряда, в противном случае считают, что у данной СВ нет математического ожидания.