Появления события

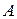
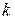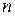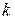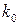Выше мы рассмотрели формулу Бернулли, которая используется для вычисления вероятности появления события раз среди независимых испытаний. Но можно рассматривать как функцию, зависящую от переменной . Функция при некотором достигает наибольшего значения. Тогда число 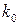называют наиболее вероятным числом появления события 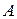при 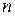испытаниях.

Определение 5.6. Наиболее вероятное число появления события 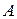при 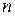испытаниях находится по формуле

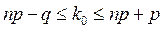. (6.6)

Пример 6.5. На заводе допускается брак в продукции с вероятностью, равной 0,022. Изготовлено 4500 единиц продукции. Найти наиболее вероятное число единиц продукции, удовлетворяющее стандарту.

Решение. По условию 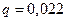, тогда .

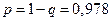По формуле наиболее вероятного числа находим

;

.

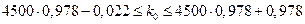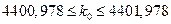Откуда k₀=4401.

,

6. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

ДИСКРЕТНЫЕ СВ

Выше рассматривались события, состоящие в появлении того или иного числа в результате проведения некоторого вероятностного эксперимента. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5 и 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле появление числа очков на игральной кости есть величина случайная, т.е. числа 1, 2, 3, 4, 5 и 6 - есть возможные значения этой величины.

Определение 1. Величина, которая в зависимости от случая может принимать те или другие числовые значения, называется случайной.

Надо отметить то, что случайные величины (сокращенно СВ) - есть математические модели вероятностных экспериментов.

Примерами случайных величин являются: количество деталей высокого качества, сошедших с конвейера в течение смены; количество зерен в случайно взятом колосе; результат измерения длины, массы, времени и т.д.

Уже из рассмотренных примеров можно заключить о целесообразности различать случайные величины, принимающие лишь отдельные, изолированные значения и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. Поэтому рассматривают дискретные и непрерывные случайные величины (обозначаются кратко СВ).

Определение 2. Дискретной (прерывной) (обозначаются ДСВ) называется случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений ДСВ может быть конечным или бесконечным.

Определение 3. Непрерывной (обозначается НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений НСВ – бесконечно.

Замечание: Настоящее определение НСВ не является точным. Более строгое определение будет дано позднее.

В дальнейшем случайные величины будем обозначать заглавными буквами латинского алфавита X, Y, Z и т.д. Значения, которые эти величины могут принимать, обозначаются малыми буквами x, y, z, a, b, a, b и т.д.