Закон распределения ДСВ.

Значения ДСВ можно записать в виде конечной или бесконечной последовательности 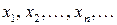. Для каждого из этих значений 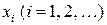определяют соответствующую вероятность .

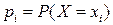Определение 6.1. Законом распределения ДСВ называют соответствие между возможными значениями СВ 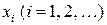и их вероятностями .

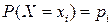Закон распределения ДСВ можно задать таблично, аналитически (в виде формулы) и графически.

Если закон распределения ДСВ задают таблично, иначе называют рядом распределения, то таблица принимает следующий вид:

Таблица 6.1

			…		…
			…		…

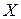
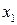
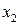
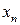
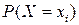
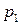
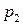
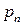
Для ряда распределения должны выполняться два требования:

1) (вероятности не могут быть отрицательными величинами);

2) .

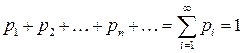Если X принимает конечное число значений, то такая ДСВ называется конечнозначной.

В целях наглядности закон распределения ДСВ можно изобразить и графически, для чего в прямоугольной системе координат строят точки , а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

Закон распределения ДСВ задается еще функцией распределения.

Определение 6.2. Для ДСВ X с законом распределения 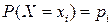функция распределения имеет вид

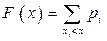, (6.1)

где суммирование распространяется на все те индексы 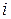, для которых .

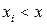Графиком функции распределения для ДСВ является кусочно-постоянная функция.