Свойства потока событий
1) Свойство стационарности характеризуется тем, что вероятность появления  событий на любом промежутке времени зависит только от числа
событий на любом промежутке времени зависит только от числа  и от длительности
и от длительности 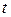 промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися.
промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися.
Итак, если поток обладает свойством стационарности, то вероятность появления  событий за промежуток времени длительности
событий за промежуток времени длительности 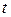 есть функция, зависящая только от
есть функция, зависящая только от  и
и 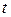 .
.
2) Свойство «отсутствие последействия» характеризуется тем, что вероятность появления  событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в момент времени, предшествующий началу рассматриваемого промежутка.
событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в момент времени, предшествующий началу рассматриваемого промежутка.
Итак, если поток обладает свойством отсутствия последействия, то имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени.
3) Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно.
Итак, если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события.
Определение 5.3. Простейшим (пуассоновским) называется поток событий, который обладает свойством стационарности, отсутствия последействия и ординарности.
Определение 5.4. Интенсивностью потока l называют среднее число событий, которое появляется в единицу времени.
Определение 5.5. Вероятность появления 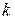 событий простейшего потока с постоянной интенсивностью
событий простейшего потока с постоянной интенсивностью 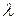 за время длительности
за время длительности 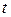 определяется формулой Пуассона:
определяется формулой Пуассона:
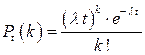 . (5.5)
. (5.5)
Эта формула отражает все свойства простейшего потока.
Пример 5.4. При работе прибора поток неисправностей можно считать простейшим. Среднее число неисправностей за сутки равно 2. Найти вероятность того, что за двое суток возникнет более двух неисправностей.
Решение. Пусть 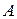 - событие, заключающееся в том, что за две суток возникнет более двух неисправностей. Тогда
- событие, заключающееся в том, что за две суток возникнет более двух неисправностей. Тогда 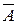 - событие, заключающееся в том, что за двое суток возникнет число неисправностей менее или равное двум.
- событие, заключающееся в том, что за двое суток возникнет число неисправностей менее или равное двум.
По условию задачи: 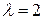 ,
, 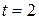 ,
, 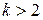 . Тогда
. Тогда
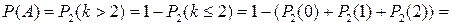
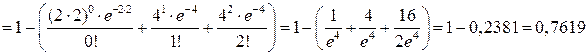 .
.
,
Дата добавления: 2015-10-09; просмотров: 759;
