Формула Пуассона. Пусть производится независимых испытаний, в каждом из которых вероятность появления события равна
Пусть производится 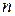 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 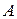 равна
равна 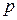 . Для определения вероятности
. Для определения вероятности  появлений события в этих испытаниях используют формулу Бернулли. Если же
появлений события в этих испытаниях используют формулу Бернулли. Если же 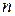 велико, то пользуются асимптотической формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала
велико, то пользуются асимптотической формулой Лапласа. Однако, эта формула непригодна, если вероятность события мала 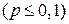 . В этих случаях, когда
. В этих случаях, когда 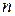 велико, а
велико, а 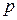 мало, прибегают к асимптотической формуле Пуассона.
мало, прибегают к асимптотической формуле Пуассона.
Итак, поставим своей задачей найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно  раз.
раз.
Сделаем важное допущение: произведение 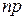 сохраняет постоянное значение, а именно
сохраняет постоянное значение, а именно 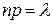 . Как будет следовать из дальнейшего, это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях
. Как будет следовать из дальнейшего, это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях 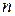 , остается неизменным.
, остается неизменным.
Теорема 5.3 (формула Пуассона).
Пусть вероятность события 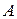 при каждом из
при каждом из 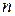 независимых испытаний равна
независимых испытаний равна 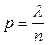 , где
, где 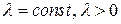 . Тогда
. Тогда
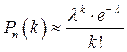 . (5.4)
. (5.4)
Данную теорему примем без доказательства.
Пример 5.3. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредиться, равна 0,0002. Найти вероятность того, что на базу прибудет более трех поврежденных изделий.
Решение. По условию n=5000, p=0,0002. Найдем l:
l=np=5000×0,0002=1.
Пусть A – событие, состоящее в том, что на базу прибудет более трех поврежденных изделий. Тогда 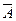 - противоположное событию A заключается в том, что на базу прибудет менее или равное трем количество поврежденных изделий, т.е.
- противоположное событию A заключается в том, что на базу прибудет менее или равное трем количество поврежденных изделий, т.е. 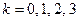 . А значит, вероятность события A находится следующим образом
. А значит, вероятность события A находится следующим образом
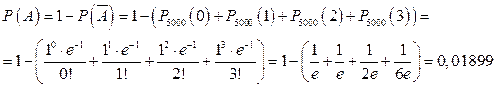
,
Дата добавления: 2015-10-09; просмотров: 607;
