Формула Бернулли. Приближенная формула Муавра - Лапласа
Если производится несколько испытаний, причем вероятность события 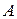 в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события
в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события 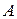 .
.
В разных независимых испытаниях событие 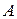 может иметь либо различные вероятности, либо одну и ту же вероятность. Мы будем далее рассматривать лишь такие независимые испытания, в которых событие
может иметь либо различные вероятности, либо одну и ту же вероятность. Мы будем далее рассматривать лишь такие независимые испытания, в которых событие 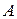 имеет одну и ту же вероятность.
имеет одну и ту же вероятность.
Пусть производится 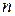 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие 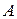 может появиться либо не появиться. Будем считать, что вероятность события
может появиться либо не появиться. Будем считать, что вероятность события 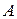 в каждом испытании одна и та же, а именно равно
в каждом испытании одна и та же, а именно равно 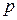 . Следовательно, вероятность не наступления события
. Следовательно, вероятность не наступления события 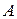 в каждом испытании также постоянна и равна
в каждом испытании также постоянна и равна 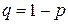 .
.
Поставим своей задачей вычислить вероятность того, что при 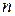 испытаниях событие
испытаниях событие 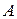 осуществиться ровно
осуществиться ровно  раз и, следовательно, не осуществиться
раз и, следовательно, не осуществиться 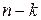 раз.
раз.
Важно подчеркнуть, что не требуется, чтобы событие 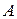 повторялось ровно
повторялось ровно  раз в определенной последовательности. Например, если речь идет о появлении события
раз в определенной последовательности. Например, если речь идет о появлении события 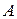 три раза в четырех испытаниях, то возможны следующие сложные события:
три раза в четырех испытаниях, то возможны следующие сложные события:
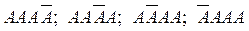 .
.
Искомую вероятность обозначим 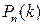 . Например, символ
. Например, символ 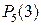 означает вероятность того, что в пяти испытаниях событие появилось 3 раза и, следовательно, не наступило 2 раза.
означает вероятность того, что в пяти испытаниях событие появилось 3 раза и, следовательно, не наступило 2 раза.
Поставленную задачу решает так называемая формула Бернулли.
Определение 5.1 (формула Бернулли).
Пусть производится n независимых испытаний. Вероятность появления события A в каждом испытании равна p. Тогда вероятность появления события A при n испытаниях ровно k раз находится по формуле:
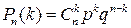 . (5.1)
. (5.1)
Пример 5.1. В проверочном тесте по русскому языку для каждого из десяти вопросов предлагается пять ответов (один из которых правильный). Какова вероятность того, что будут правильно даны ответы:
- на восемь вопросов;
- хотя бы на восемь вопросов.
Приближенная формула Муавра - Лапласа (локальная).
При большом значении n применение формулы Бернулли затруднительно. Тогда используют формулу Муавра- Лапласа. Муавр доказал частный случай для p=1/2.
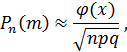
где
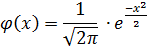
- функция Лапласа, значения в таблице № 1.
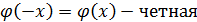
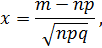
если 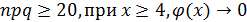 ,
, 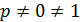
Пример.
Установлено, что 94% лиц, которым сделали прививку от туберкулеза, приобретают иммунитет.
Найти вероятность того, что среди 100000 граждан, которым делали прививки, 5800 не защищены от туберкулеза.
Решение:
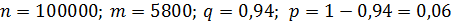
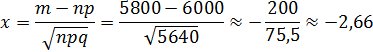
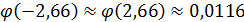
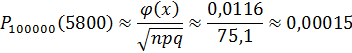
Дата добавления: 2015-10-09; просмотров: 900;
