Теорема 3.4.

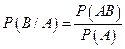. (3.4)

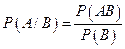. (3.5)

Сформулируем теорему умножения вероятностей, приняв ее без доказательства.

Теорема 3.5 (теорема умножения вероятностей).

Вероятность совместного наступления двух событий (вероятность произведения двух событий) равна произведению вероятности одного из них на условную вероятность другого при условии, что первое уже произошло.

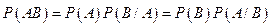. (3.6)

Пример 3.2. Из урны, в которой m черных и n белых шаров, извлекают два шара. Чему равна вероятность того, что:

а) оба шара белых;

б) шары разного цвета.

Решение. а) Пусть A₁ – событие, состоящее в том, что первый шар белый, A₂ – событие, состоящее в том, что второй шар белый. Тогда

.

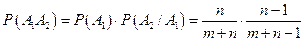б) Пусть A₁B₂ – событие, состоящее в том, что первый шар белый, а второй – черный, B₁A₂ – событие, состоящее в том, первый шар черный, а второй – белый. Тогда

,

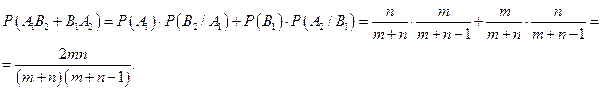
Теорему умножения вероятностей легко распространить на случай, когда событий больше двух.

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

,

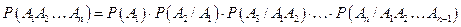где 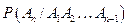– вероятность события A_n, вычисленная в предположении, что события A₁, A₂, …, A_n-1 наступили.

В частности для трех событий будем иметь: .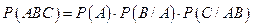

Заметим, что порядок, в котором расположены события, может быть выбран любым. Безразлично, какое событие считать первым, вторым и т.д.

Определение 3.1. Два события называются независимыми, если вероятность одного из них не зависит от появления или не появления другого, т.е.

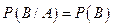или .

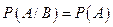Два события называются зависимыми, если вероятность появления одного из них зависит от наступления или не наступления другого события.

Теорема умножения вероятностей, которая была доказана выше, рассматривалась для зависимых событий. Сформулируем теорему умножения вероятностей (без доказательства) для независимых событий.

Теорема 3.6. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

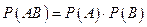. (3.7)

Пример 3.3. Студент может уехать в университет или автобусом, который ходит через каждые 20 мин, или маршрутным такси, которое ходит через каждые 10 мин. Какова вероятность того, что студент, подошедший к остановке, уедет в течение ближайших пяти минут?

Решение. Пусть A – событие, заключающееся в том, что студент, подошедший к остановке, уедет в течение ближайших пяти минут. Событие A будет состоять из двух совместных событий: A₁ – событие, состоящее в том, что студент в течение пяти минут уедет автобусом; A₂ – событие, состоящее в том, что студент в течение пяти минут уедет маршрутным такси. Совместность этих событий заключается в том, что к остановке одновременно может подойти как автобус, так и маршрутное такси. Но эти события независимые. Поэтому по т.3.2. и по т.3.6. имеем

.

,

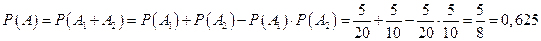Пусть в результате испытания может появиться n событий независимых в совокупности, либо некоторые их них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема, которую примем без доказательства.

Теорема 3.7. Вероятность появления хотя бы одного из событий A₁, A₂, …, A_n, независящих в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :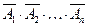

.

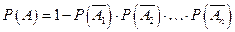Пример 3.4. (Условие примера 3.1.) На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете;

Решение. 1) Пусть A – событие, заключающееся в том, что хотя бы один из трех отобранных учебников будет в переплете. Рассмотрим противоположное событие 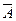- состоящее в том, что ни один из трех взятых учебников не будет в переплете. События A и 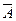образуют полную группу событий. Значит, 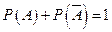. Тогда

.

,

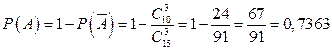Пример 3.5. Вероятности попадания в цель при стрельбе из трех орудий таковы: p₁=0,8, p₂=0,7, p₃=0,9. Найти вероятность:

а) только одного попадания при одном залпе из всех орудий;

б) хотя бы одного попадания при одном залпе из всех орудий.

Решение. а) Пусть A – событие, состоящее в том, что при одном залпе из всех орудий было только одно попадание. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий. Событие A возможно при появлении одного из попарно несовместных событий A₁, или A₂, или A₃.

A₁ – событие, состоящее в том, что произошло попадание в цель первым орудием, т.е. первое орудие попало, второе и третье – нет, значит, ;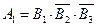

A₂ – событие, состоящее в том, что произошло попадание в цель вторым орудием, т.е. второе орудие попало, а первое и третье – нет, ;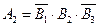

A₃ – событие, состоящее в том, что произошло попадание в цель третьим орудием, т.е. третье орудие попало, а первое и второе – нет, .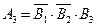

Таким образом, получаем .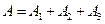

События B₁, B₂, B₃ независимы. Используя теоремы сложения и умножения вероятностей, получаем:

,

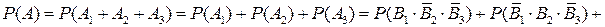
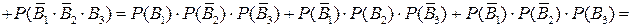
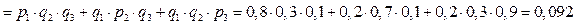где q₁, q₂, q₃ – соответствующие вероятности промаха каждым орудием.

б) Пусть C – событие, состоящее в том, что при одном залпе из всех орудий было хотя бы одно попадание. Рассмотри противоположное событие 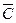, состоящее в том, что при одном залпе не было ни одного попадания, т.е. 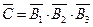. События C и 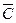образуют полную группу, поэтому сумма их вероятностей равна единице. Следовательно, получаем

.

,

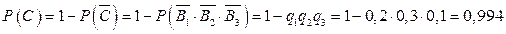Теоремы сложения и умножения вероятностей широко используются при расчете вероятности безотказной работы или вероятности разрыва электрической цепи, если даны, например, вероятности отказа каждого узла, входящего в электрическую схему. Как известно, соединения приборов в электрической цепи возможно двумя способами: параллельным или последовательным.

4. ФОРМУЛА ПОЛНОЙ ВЕРОЯНОСТИ.

ФОРМУЛА БАЙЕСА