Теорема сложения вероятностей
Теорема 3.1. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
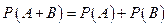 . (3.1)
. (3.1)
Доказательство. Введем обозначения:
n – общее число возможных элементарных исходов испытания;
m1 – число исходов, благоприятствующих событию A;
m2 – число исходов, благоприятствующих событию B.
Число элементарных исходов, благоприятствующих наступлению либо события A, либо события B, равно m1+m2. Следовательно,
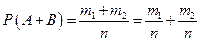 .
.
Приняв во внимание, что 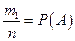 и
и 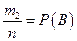 , окончательно получаем
, окончательно получаем
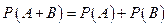 .
.
,
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
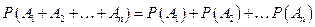 .
.
Теорема 3.2. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
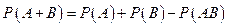 . (3.2)
. (3.2)
Данную теорему примем без доказательства.
Теорема 3.3. Сумма вероятностей противоположных событий равна единице:
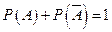 . (3.3.)
. (3.3.)
Доказательство. Противоположные события образуют полную группу, а сумма вероятностей событий, образующих полную группу, равна единице.
,
Пример 3.1. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы два учебника окажется в переплете;
Решение. 1) Пусть A – событие, заключающееся в том, что хотя бы два учебника из трех отобранных будет в переплете. Событие A будет состоять из двух несовместных событий: A1 – событие, состоящее в том, что из трех отобранных учебников два в переплете, а один – нет; A2 – событие, состоящее в том, что из трех отобранных учебников все три в переплете. Тогда 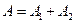 .
.
Поскольку события A1 и A2 несовместны, то по т. 3.1. получаем
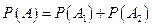 .
.
Вероятности событий A1 и A1 находим, используя классическое определение вероятностей.
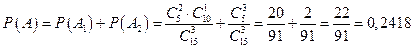 .
.
,
Дата добавления: 2015-10-09; просмотров: 617;
