Классическая вероятность
Рассмотрим пространство W, связанное с каким-либо опытом, состоящим из конечного числа n элементарных событий. Дополнительно будем предполагать, что все элементарные события равновозможные, то есть, если есть основания считать, что ни одно из этих событий не является более возможным, чем другие. Как правило, равновозможность является следствием симметрии предметов, участвующих в эксперименте. Примеры опытов с равновозможными исходами: вытаскивание карты из колоды; выбор товара при покупке; заполнение карточки спортлото и др. Равновозможные элементарные события, образующие пространство W, называют исходами (случаями, шансами) данного опыта.
Определение 2.1 (классическое определение вероятности).
Пусть задан вероятностный эксперимент с конечным числом элементов в 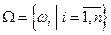 , в котором элементарные события wi равновероятны, т.е.
, в котором элементарные события wi равновероятны, т.е. 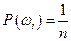 . Тогда вероятность события P(A) – есть отношение числа элементарных событий, благоприятствующих для A, к общему числу элементарных событий в W:
. Тогда вероятность события P(A) – есть отношение числа элементарных событий, благоприятствующих для A, к общему числу элементарных событий в W:
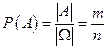 . (2.1)
. (2.1)
Пример 2.1. В лифт 9-этажного дома входят 4 человека. Какова вероятность того, что они выйдут на разных этажах?
Решение. Пусть A – событие, заключающееся в том, что четыре человека выйдут на разных этажах. Так как каждый пассажир лифта может выйти на любом из этажей, то число всех возможностей равно 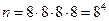 , что соответствует всему числу испытаний.
, что соответствует всему числу испытаний.
Теперь подсчитаем число благоприятных исходов испытаний. У первого пассажира лифта есть 8 возможностей выйти (на этажах 2-9), тогда у второго остается 7 возможностей, у третьего – 6 и у четвертого – 5. Значит, 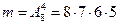 .
.
Поэтому 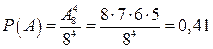 .
.
,
Пример 2.2. На шести карточках написаны буквы К, Л, О, О, П, Ц. Карточки перемешивают и наугад раскладывают в ряд. Какова вероятность того, что получится слово ПОЛОЦК? Какова вероятность того, что получится слово ПОЛК?
Решение. Пусть A – событие, заключающееся в том, что получится слово ПОЛОЦК. Из шести различных элементов можно составить P6=6!=720 перестановок. Значит, всего равновозможных исходов будет n=720. Корточки с буквами, отличными от буквы О, могут стоять на определенных местах. Две буквы О можно расположить на двух местах 2!=2 способами. Поэтому число благоприятных данному событию будет m=2. Следовательно, 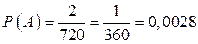 .
.
Пусть B – событие, заключающееся в том, что получится слово ПОЛК. Число всех исходов испытания равно числу размещений из шести элементов по четыре, а число благоприятных данному событию равно числу перестановок буквы О. Таким образом 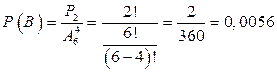 .
.
,
Пример 2.3. В ящике находится 10 шаров, из которых 7 красного цвета, а остальные белого. Найти вероятность того, что среди шести взятых наудачу шаров, ровно 4 красного цвета.
Решение.Пусть A – событие, заключающееся в том, что среди шести взятых наудачу шаров, ровно 4 красного цвета. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 шаров из 10, т.е. числу сочетаний из 10 элементов по 6, 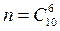 .
.
Подсчитаем число исходов, благоприятствующих интересующему нас событию A. 4 шара красного цвета можно взять из 7 шаров красного цвета 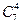 способами; при этом остальные 6-4=2 шара должны быть белого цвета; взять же 2 шара белого цвета из 10-7=3 белых шаров можно
способами; при этом остальные 6-4=2 шара должны быть белого цвета; взять же 2 шара белого цвета из 10-7=3 белых шаров можно 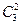 способами. Следовательно, число благоприятных исходов равно
способами. Следовательно, число благоприятных исходов равно 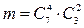 .
.
Поэтому 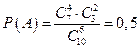 . ,
. ,
Дата добавления: 2015-10-09; просмотров: 700;
