Геометрическая вероятность. Классическое определение вероятности нельзя применять к опыту с бесконечным числом равновероятных исходов
Классическое определение вероятности нельзя применять к опыту с бесконечным числом равновероятных исходов. Чтобы преодолеть недостаток классического определения вероятности, состоящей в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности – вероятности попадания точки в область.
Определение 2.2 (геометрическое определение вероятности).
Пусть W - ограниченное множество n-мерного евклидова пространства. Элементарные события трактуем как точки 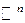 , n=1, 2, 3, …, события трактуем как подпространства из
, n=1, 2, 3, …, события трактуем как подпространства из 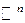 . Тогда
. Тогда
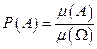 , (2.2)
, (2.2)
где m означает длину для  , площадь для
, площадь для 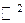 , объем для
, объем для 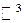 .
.
Пример 2.4. (Задача о встрече) Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет второго в течение 15 мин, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 12 до 13 часов).
Решение.Пусть x – момент прихода 1-го студента в течение часа, y – момент прихода 2-го студента в течение часа, где 0£ x £1, 0£ y £1. Тогда время прихода двух студентов можно рассматривать как точки пространства R2. Всего исходов испытания – это множество точек расположенных в квадрате OABC. Поэтому m(W)=SOABC=1.
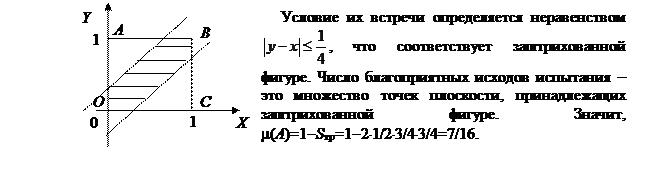
Поэтому 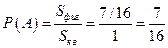 .
.
,
Из определения вероятности вытекают следующая теорема, которую примем без доказательства.
Теорема 2.1. Вероятность любого события 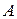 удовлетворяет неравенству
удовлетворяет неравенству
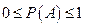 .
.
Дата добавления: 2015-10-09; просмотров: 876;
