Формула полной вероятности. Пусть событие A может наступить при условии появления одного из несовместных событий H1, H2, , Hn, которые образуют полную группу
Пусть событие A может наступить при условии появления одного из несовместных событий H1, H2, …, Hn, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности P(A/H1), …, P(A/Hn) события A. Как найти вероятность события A? Ответ на этот вопрос дает следующая теорема, которую примем без доказательства.
Теорема 4.1 (формула полной вероятности).
Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий H1, H2, …, Hn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
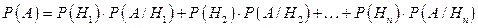 . (4.1)
. (4.1)
Пример 4.1. В обувной магазин на продажу поступила обувь марки «Белвест» и «Марко». Продукция марки «Белвест» содержит 2 % скрытого дефекта, а марки «Марко» - 1,5 %. Какова вероятность приобрести пару обуви со скрытыми дефектами, если в магазин поступило 40 % пар обуви марки «Белвест», а остальные марки «Марко».
Решение. Пусть A – событие, состоящее в том, что приобретенная пара обувь со скрытыми дефектами. H1 – событие, состоящее в том, что куплена пара обуви марки «Белвест», H2 – купленная пара обуви марки «Марко». Тогда
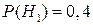 ;
; 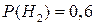 .
.
Пусть 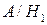 - событие, заключающееся в том, что купленная пара обуви марки «Белвест» имеет скрытые дефекты;
- событие, заключающееся в том, что купленная пара обуви марки «Белвест» имеет скрытые дефекты; 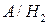 - событие, заключающееся в том, что купленная пара обуви марки «Марко» имеет скрытые дефекты. Тогда
- событие, заключающееся в том, что купленная пара обуви марки «Марко» имеет скрытые дефекты. Тогда
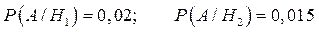 .
.
По формуле (4.1) искомая вероятность
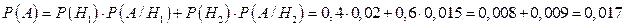 ,
,
Дата добавления: 2015-10-09; просмотров: 599;
