Формула Байеса. Пусть событие A может наступить при условии появления одного из несовместных событий H1, H2, , Hn, образующих полную группу

Пусть событие A может наступить при условии появления одного из несовместных событий H₁, H₂, …, H_n, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность события A определяется по формуле полной вероятности. Требуется найти вероятность гипотезы H_i при условии, что событие A уже произошло.

По формуле условной вероятности имеем:

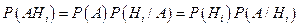
или

.

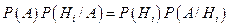Откуда получаем

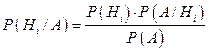, (4.2)

где P(A) – формула полной вероятности.

Формула (4.2) называется формулой Байеса (по имени английского математика). Формула Байеса позволяет переоценить вероятности гипотез после того, как станет известным результат испытания, в итоге которого появилось событие A.

Если доопытные вероятности гипотез неизвестны, их полагают одинаковыми: P(H₁)=P(H₂)=…=P(H_n). В таком случае формула Байеса принимает вид

.

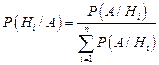Пример 4.2. 40% приборов собирается из высококачественных деталей, остальные – из деталей обычного качества. В первом случае надежность прибора (вероятность безотказной работы) за время Т равна 0,90; если прибор из обычных деталей, его надежность равна 0,60. Прибор в течение времени Т работал безотказно. Чему равна вероятность того, что он собран из высококачественных деталей?

Решение. Возможны две гипотезы: H₁ – прибор собран из высококачественных деталей; H₂ – прибор собран из обычных деталей. Из условия имеем:

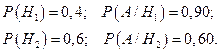
Здесь A – событие, состоящее в том, что прибор безотказно работал в течение времени T.

Нас интересует P(H₁/A). По формуле Байеса получаем

.

,

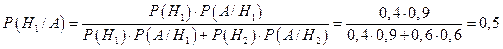Пример 4.3. Имеется три урны. В первой находится 3 белых и 5 черных шаров, во второй – 4 белых и 3 черных, в третьей – 5 белых и 6 черных. Найти вероятность того, что, если выбранный шар оказался белого цвета, то какова вероятность того, что он был взят из второй урны?

Решение. Возможны три гипотезы: H₁ – шар взят из первой урны; H₂ – шар взят из второй урны; H₃ – шар взят из третьей урны. Из условия имеем:

.

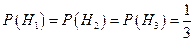Событие A – событие, состоящее в том, что шар из наугад выбранной урны окажется белым.

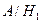– событие, состоящее в том, что шар, извлеченный из первой урны, окажется белым; 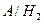- событие, состоящее в том, что шар, извлеченный из второй урны, окажется белым; 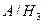- событие, состоящее в том, что шар, извлеченный из третьей урны, окажется белым.

; ; .

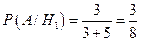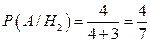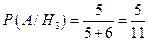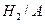– событие, состоящее в том, что извлеченный белый шар оказался взят из второй урны. По формуле Байеса получаем

,

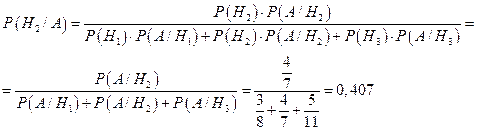
Пример 4.4.В магазин на продажу поступили электрочайники, изготовленные на двух заводах. Вероятность того, что электрочайник, изготовленный на первом заводе, прослужит гарантийный срок, равна 0,82, а электрочайник, изготовленный на втором заводе – 0,79. Всего поступило 45 % продукции с завода № 1, а остальные - с завода № 2.

1) Найти вероятность того, что приобретенный электрочайник прослужит гарантийный срок.

2) Чайник прослужил гарантийный срок. На каком заводе он вероятнее всего изготовлен?

Решение. 1) Пусть A – событие, состоящее в том, что приобретенный электрочайник прослужит гарантийный срок. H₁ – событие, состоящее в том, что куплен электрочайник, изготовленный на заводе № 1, H₂ – куплен электрочайник, изготовленный на заводе № 2. Тогда

; .

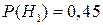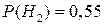Пусть 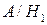- событие, заключающееся в том, что купленный электрочайник, изготовленный на первом заводе, прослужит гарантийный срок; 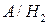- событие, заключающееся в том, что купленный электрочайник, изготовленный на втором заводе, прослужит гарантийный срок. Тогда

.

По формуле (4.1) искомая вероятность

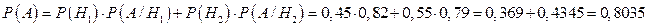
2) 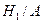– событие, состоящее в том, что купленный качественный электрочайник изготовлен на заводе № 1, 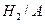− событие, состоящее в том, что купленный качественный электрочайник изготовлен на заводе № 2. По формуле Байеса получаем

,

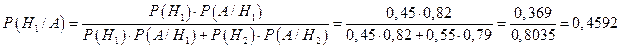
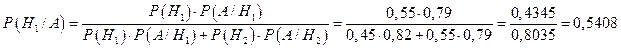
5. ПОВТОРЕНИЕ ИСПЫТАНИЙ