Вероятность события

Теория вероятностей, так же как и другие разделы математики, имеет дело не с явлениями окружающего мира непосредственно, а с их математическими моделями. Построение математической модели вероятностного эксперимента происходит в следующей последовательности:

1) составляется пространство элементарных событий W вероятностного эксперимента;

2) выделяется класс событий F, достаточных для описания закономерностей изучаемого явления;

3) определяется степень возможности появления событий из класса F, т.е. вводится вероятностная мера для наступления событий. Эту меру события A из F называют вероятностью появления события A и обозначают P(A). Саму модель тогда обозначают (W, F, P).

Определение 1.11. Класс F как множество всех подмножеств из W называют алгеброй событий, если выполняются следующие аксиомы:

(1) WÎF;

(2) ;

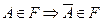(3) .

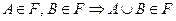Кстати, из условий (2) и (3) следует, что пересечение и разность событий также принадлежат F.

Пример 1.5. Пусть 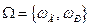- полная группа элементарных событий при подбрасывании монеты один раз. Тогда

.

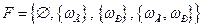Так как 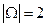, то .

,

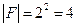Определение 1.12. Пусть W - пространство элементарных событий для заданного вероятностного эксперимента, F - алгебра событий, выделенная в W. Действительная функция P, ставящая каждому событию A в соответствие число P(A), называется вероятностной мерой на F, если выполняются следующие аксиомы (А.Н. Колмогорова, 1933):

А1. ;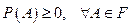

А2. Если A=W, то P(W)=1;

А3. Для любой последовательности попарно несовместных событий A₁, A₂, …, A_n,…, где 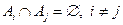выполняется соотношение

.

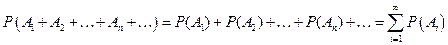Иначе P(A) называют вероятностью события A.

2. КЛАССИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ

ВЕРОЯТНОСТИ