Линейные операторы
Линейным оператором (преобразованием, отображением) n-мерного векторного пространства называется правило Y = f(X), по которому каждому вектору Х ставится в соответствие единственный вектор Y, причем сохраняются линейные операции над векторами, т.е. имеют место свойства:
1) f(X + Z) = f(X) + f(Z) - свойство аддитивности оператора;
2) f(lX) = lf(X) - свойство однородности оператора.
Можно доказать, что каждому линейному оператору соответствует квадратная матрица в данном базисе. Справедливо и обратное: всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.
Поэтому линейное преобразование можно определить по-другому: линейным оператором n-мерного векторного пространства, заданным квадратной матрицей А, называется преобразование, которое любому вектору X, записанному в виде матрицы-столбца 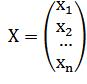 , ставит в соответствие вектор А(Х) = А*Х =
, ставит в соответствие вектор А(Х) = А*Х = 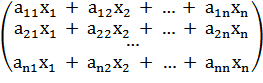 .
.
Матрицу А называют матрицей оператора в данном базисе, а ранг этой матрицы - рангом оператора.
Например, если линейный оператор задан матрицей 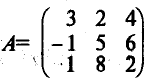 , то отображение Y вектора X = (4, -3, 1) будет равно
, то отображение Y вектора X = (4, -3, 1) будет равно
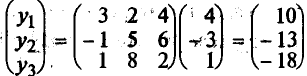 .
.
Отметим, что единичная матрица задает тождественное преобразование (тождественный оператор), поскольку, умножая ее на вектор, мы получаем тот же самый вектор.
Нулевая матрица определяется, как нулевой оператор, переводящий все векторы пространства в нулевые векторы.
Легко убедиться, что диагональная матрица, на диагонали которой стоит одно и то же число, задает оператор умножения вектора на это число.
Теорема. Матрицы А и А* одного и того же линейного оператора в базисах el, e2,...en и el*, e2*,...en* связаны соотношением А* = С-1АС, где С - матрица перехода от старого базиса к новому.
Доказательство. Обозначим Y отображение вектора X в базисe
el, e2,...en, а те же вектора в базисе el*, e2*,...en* обозначим Х* и Y*. Так как С - матрица перехода, можно записать:
X = СХ*
Y = CY*
Умножим слева обе части первого равенства на матрицу А:
АX = АСХ*
Так как АX = Y, получим Y = АСХ*, т.е. CY* = АСХ*. Домножив обе части последнего равенства на С-1, получим:
С-1CY* = С-1АСХ*
Y* = С-1АСХ*.
Так как Y* = А*X*, А* = С-1АС, что и требовалось доказать.
Например, пусть в базисе el, e2 матрица оператора А = 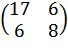 . Найти матрицу этого оператора в базисе el* = el -2e2, e2 = 2el + e2.
. Найти матрицу этого оператора в базисе el* = el -2e2, e2 = 2el + e2.
Для этого построим матрицу перехода С = 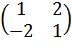 и обратную ей матрицу С-1. |C| = 5,
и обратную ей матрицу С-1. |C| = 5, 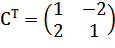 , r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 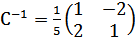 . Тогда
. Тогда
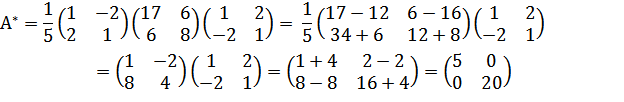
Дата добавления: 2015-10-06; просмотров: 978;
