Собственные векторы и собственные значения линейного оператора
Вектор Х ≠ 0 называют собственным вектором линейного оператора с матрицей А, если найдется такое число l, что АХ = lХ.
При этом число l называют собственным значением оператора (матрицы А), соответствующим вектору х.
Иными словами, собственный вектор – это такой вектор, который под действием линейного оператора переходит в коллинеарный вектор, т.е. просто умножается на некоторое число. В отличие от него, несобственные векторы преобразуются более сложно.
Запишем определение собственного вектора в виде системы уравнений:
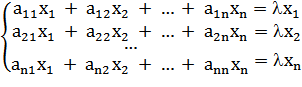
Перенесем все слагаемые в левую часть:
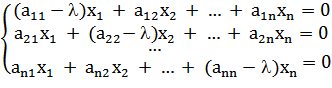
Последнюю систему можно записать в матричной форме следующим образом:
(А - lЕ)Х = О
Полученная система всегда имеет нулевое решение Х = О. Такие системы, в которых все свободные члены равны нулю, называют однородными. Если матрица такой системы – квадратная, и ее определитель не равен нулю, то по формулам Крамера мы всегда получим единственное решение – нулевое. Можно доказать, что система имеет ненулевые решения тогда и только тогда, когда определитель этой матрицы равен нулю, т.е.
|А - lЕ| = 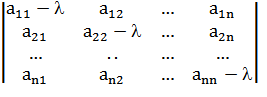 = 0
= 0
Это уравнение с неизвестным l называют характеристическим уравнением (характеристическим многочленом) матрицы А (линейного оператора).
Можно доказать, что характеристический многочлен линейного оператора не зависит от выбора базиса.
Например, найдем собственные значения и собственные векторы линейного оператора, заданного матрицей А = 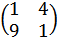 .
.
Для этого составим характеристическое уравнение |А - lЕ| = 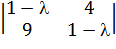 = (1 - l)2 – 36 = 1 – 2l + l2 - 36 = l2 – 2l - 35; Д = 4 + 140 = 144; собственные значения l1 = (2 - 12)/2 = -5; l2 = (2 + 12)/2 = 7.
= (1 - l)2 – 36 = 1 – 2l + l2 - 36 = l2 – 2l - 35; Д = 4 + 140 = 144; собственные значения l1 = (2 - 12)/2 = -5; l2 = (2 + 12)/2 = 7.
Чтобы найти собственные векторы, решаем две системы уравнений
(А + 5Е)Х = О
(А - 7Е)Х = О
Для первой из них расширенная матрица примет вид
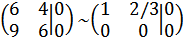 ,
,
откуда х2 = с, х1 + (2/3)с = 0; х1 = -(2/3)с, т.е. Х(1) = (-(2/3)с; с).
Для второй из них расширенная матрица примет вид
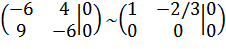 ,
,
откуда х2 = с1, х1 - (2/3)с1 = 0; х1 = (2/3)с1, т.е. Х(2) = ((2/3)с1; с1).
Таким образом, собственными векторами этого линейного оператора являются все вектора вида (-(2/3)с; с) с собственным значением (-5) и все вектора вида ((2/3)с1; с1) с собственным значением 7.
Можно доказать, что матрица оператора А в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
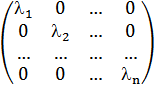 ,
,
где li – собственные значения этой матрицы.
Верно и обратное: если матрица А в некотором базисе является диагональной, то все векторы этого базиса будут собственными векторами этой матрицы.
Также можно доказать, что если линейный оператор имеет n попарно различных собственных значений, то соответствующие им собственные векторы линейно независимы, а матрица этого оператора в соответствующем базисе имеет диагональный вид.
Поясним это на предыдущем примере. Возьмем произвольные ненулевые значения с и с1, но такие, чтобы векторы Х(1) и Х(2) были линейно независимыми, т.е. образовали бы базис. Например, пусть с = с1 = 3, тогда Х(1) = (-2; 3), Х(2) = (2; 3). Убедимся в линейной независимости этих векторов:
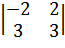 = -12 ≠ 0. В этом новом базисе матрица А примет вид А* =
= -12 ≠ 0. В этом новом базисе матрица А примет вид А* = 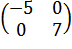 .
.
Чтобы убедиться в этом, воспользуемся формулой А* = С-1АС. Вначале найдем С-1.
СТ = 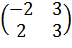 ;
;
С-1 = 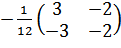 ;
;
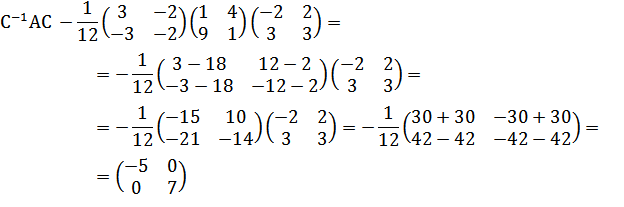
Дата добавления: 2015-10-06; просмотров: 809;
