Переход к новому базису

Пурть в пространстве R имеются два базиса: старый e_l, e₂,...e_n и новый e _l^*, e₂^*,...e_n^*. Любой вектор нового базиса можно представить в виде линейной комбинации векторов старого базиса:

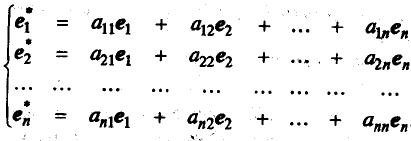
Переход от старого базиса к новому можно задать матрицей перехода

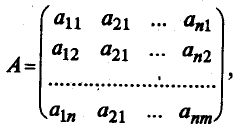
Отметим, что коэффициенты размножения новых базисных векторов по старому базису образуют столбцы, а не строки этой матрицы.

Матрица А - неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Следовательно, она имеет обратную матрицу А^-1.

Пусть вектор Х имеет координаты (х_l, х₂,... х_n) относительно старого базиса и координаты (х_l^*, х₂^*,... х_n^*) относительно нового базиса, т.е.
Х = x_le_l + x₂e₂ +...+ x_ne_n = x_l^*e_l^* + x₂^*e₂^* +...+ x_n^*e_n^*.

Подставим в это уравнение значения e_l^*, e₂^*,...e_n^* из предыдущей системы:

x_le_l + x₂e₂ +...+ x_ne_n = x_l^*(a₁₁e_l + a₁₂e₂ + … + a_1ne_n) + x₂^*(a₂₁e_l + a₂₂e₂ + … +
+ a_2ne_n) +...+ x_n^*(a_n1e_l + a_n2e₂ + … + a_nne_n)

0 = e_l( x_l^*a₁₁ + x₂^*a₂₁ + … + x_n^*a_n1 - x_l) + e₂( x_l^*a₁₂ + x₂^*a₂₂ + … + x_n^*a_n2 – x₂) +
+ … + e_n( x_l^*a_1n + x₂^*a_2n + … + x_n^*a_nn – x_n)

В силу линейной независимости векторов e_l, e₂,...e_n все коэффициенты при них в последнем уравнении должны равняться нулю. Отсюда:

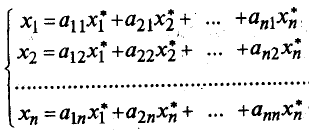
или в матричной форме

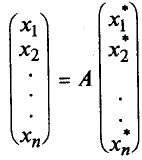
Умножим обе части на А^-1, получим:

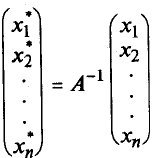
Например, пусть в базисе e_l, e₂, e₃ заданы вектора а₁ = (1, 1, 0),
а₂ = (1, -1, 1), а₃ = (-3, 5, -6) и b = (4; -4; 5). Показать, что вектора а_l, а₂, а₃ тоже образуют базис и выразить в этом базисе вектор b.

Покажем, что вектора а_l, а₂, а₃ линейно независимы. Для этого убедимся в том, что ранг составленной из них матрицы равен трем:

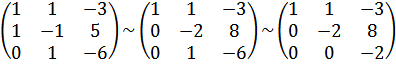
Отметим, что исходная матрица представляет собой не что иное, как матрицу перехода А. В самом деле, связь между базисами e_l, e₂, e₃ и а_l, а₂, а₃ можно выразить системой:

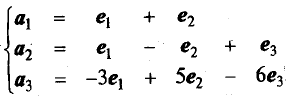
Вычислим А^-1.

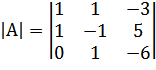= 6 + 0 - 3 – 0 – 5 + 6 = 4

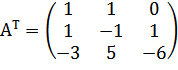
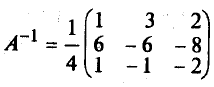
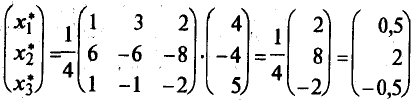
Т. е. в базисе а_l, а₂, а₃ вектор b = (0,5; 2; -0,5).